题目内容
已知在△ABC中,∠BAC=90°;分别以AB,BC为边作正方形ABDE和正方形BCFG,连接DC,GA交于点P,求证:PD⊥PG.
考点:全等三角形的判定与性质,正方形的性质
专题:证明题
分析:首先根据正方形的性质和全等三角形的判定方法可证明△ABG≌△DBC,由全等三角形的性质可得:∠BAG=∠BDC,再由正方形的性质证明∴∠P=∠E=90°即可.
解答:证明:∵四边形ABDE和四边形BCFG是正方形,
∴BG=BC,BA=BD,∠GBC=∠ABD=90°,
∴∠GBA=∠CBD,
在△ABG和△DBC中
,
∴△ABG≌△DBC,
∴∠BAG=∠BDC,
∵∠BAC=90°,
∴∠PAC+∠BAG=90°,
∵∠PAC+∠BDC=90°,∠EDC+∠BDC=90°,
∴∠PAC=∠EDC,
∴∠ACP=∠DCE,
∴∠P=∠E=90°,
∴PD⊥PG.
∴BG=BC,BA=BD,∠GBC=∠ABD=90°,
∴∠GBA=∠CBD,
在△ABG和△DBC中
|
∴△ABG≌△DBC,
∴∠BAG=∠BDC,
∵∠BAC=90°,
∴∠PAC+∠BAG=90°,
∵∠PAC+∠BDC=90°,∠EDC+∠BDC=90°,
∴∠PAC=∠EDC,
∴∠ACP=∠DCE,
∴∠P=∠E=90°,
∴PD⊥PG.
点评:本题考查了正方形的性质,全等三角形的性质和判定的应用主以及垂直的判定方法,重点考查学生的推理能力.

练习册系列答案
相关题目
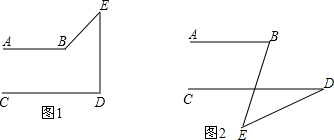 猜想:当点E在两条直线AB,CD之外时(如图1和2),∠BED,∠B,∠D满足怎样的关系时,有AB∥CD?对猜想进行证明.
猜想:当点E在两条直线AB,CD之外时(如图1和2),∠BED,∠B,∠D满足怎样的关系时,有AB∥CD?对猜想进行证明.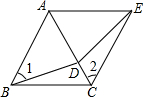 如图所示,点D为等边△ABC的AC边上的一点,∠1=∠2,BD=CE.求证:△DAE是等边三角形.
如图所示,点D为等边△ABC的AC边上的一点,∠1=∠2,BD=CE.求证:△DAE是等边三角形.