题目内容
两个三角形中,如果有两个角彼此相等,且相等的一对角的角平分线也相等,那么这两个三角形全等. (判断对错)
考点:全等三角形的判定
专题:
分析:根据题意要证明∴△ABC≌△A′B′C′,首先证明△ABD≌△A′B′D′得到AB=A′B′,进一步证明这两三角形全等.
解答: 解:如图,∵∠BAC=∠B′A′C′,AD、A′D′分别是它们的角平分线,
解:如图,∵∠BAC=∠B′A′C′,AD、A′D′分别是它们的角平分线,
∴∠BAD=∠B′AD′,
∴在△ABD与△A′B′D′中,
,
∴△ABD≌△A′B′D′(AAS),
∴AB=A′B′,
∵在△ABC与△A′B′C′中,
,
∴△ABC≌△A′B′C′(ASA).
故答案是:√
 解:如图,∵∠BAC=∠B′A′C′,AD、A′D′分别是它们的角平分线,
解:如图,∵∠BAC=∠B′A′C′,AD、A′D′分别是它们的角平分线,∴∠BAD=∠B′AD′,
∴在△ABD与△A′B′D′中,
|
∴△ABD≌△A′B′D′(AAS),
∴AB=A′B′,
∵在△ABC与△A′B′C′中,
|
∴△ABC≌△A′B′C′(ASA).
故答案是:√
点评:本题主要考查三角形全等的判定,要熟悉课本上的几种判定定理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
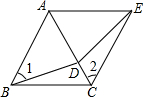 如图所示,点D为等边△ABC的AC边上的一点,∠1=∠2,BD=CE.求证:△DAE是等边三角形.
如图所示,点D为等边△ABC的AC边上的一点,∠1=∠2,BD=CE.求证:△DAE是等边三角形. 如图,CE是△ABC的外角平分线,F是CA延长线上的一点,FG∥EC交AB于G,已知∠DCE=50°,∠ABC=40°,求∠FGA的度数.
如图,CE是△ABC的外角平分线,F是CA延长线上的一点,FG∥EC交AB于G,已知∠DCE=50°,∠ABC=40°,求∠FGA的度数.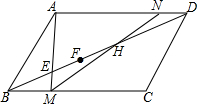 在平行四边形ABCD中,E,F,H为对角线BD上三点,且BE=EF=FH=HD,连接AE并延长交BC于点M,连接MH并延长交AD于点N,则AD:ND=
在平行四边形ABCD中,E,F,H为对角线BD上三点,且BE=EF=FH=HD,连接AE并延长交BC于点M,连接MH并延长交AD于点N,则AD:ND= 如图,把∠1,∠2,∠3按从大到小的顺序排列为
如图,把∠1,∠2,∠3按从大到小的顺序排列为