题目内容
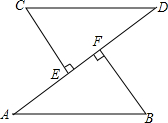 如图,AB=CD,CE⊥AD于E,BF⊥AD于F,AE=DF,求证:AB∥CD.
如图,AB=CD,CE⊥AD于E,BF⊥AD于F,AE=DF,求证:AB∥CD.考点:全等三角形的判定与性质,平行线的判定
专题:证明题
分析:求出AF=DE,再利用“HL”证明Rt△ABF和Rt△DCE全等,根据全等三角形对应角相等可得∠A=∠D,再根据内错角相等,两直线平行证明即可.
解答:证明:∵AE=DF,
∴AE+EF=DF+EF,
即AF=DE,
∵CE⊥AD,BF⊥AD,
∴∠AFB=∠DEC=90°,
在Rt△ABF和Rt△DCE中,
,
∴Rt△ABF≌Rt△DCE(HL),
∴∠A=∠D,
∴AB∥CD.
∴AE+EF=DF+EF,
即AF=DE,
∵CE⊥AD,BF⊥AD,
∴∠AFB=∠DEC=90°,
在Rt△ABF和Rt△DCE中,
|
∴Rt△ABF≌Rt△DCE(HL),
∴∠A=∠D,
∴AB∥CD.
点评:本题考查了全等三角形的判定与性质,平行线的判定,熟记三角形全等的判定方法是解题的关键,难点在于求出AF=DE.

练习册系列答案
相关题目
 在一块长35米,宽26米的矩形地面上,修建同样宽的道路如图所示(每个拐角都是直角),剩余部分栽种花草,要使剩余部分的面积为850平方米,道路的宽应为多少?
在一块长35米,宽26米的矩形地面上,修建同样宽的道路如图所示(每个拐角都是直角),剩余部分栽种花草,要使剩余部分的面积为850平方米,道路的宽应为多少?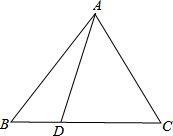 如图,在△ABC中,AB=AC,D为BC上任意一点,求证:AD2+BD•DC=AB2.
如图,在△ABC中,AB=AC,D为BC上任意一点,求证:AD2+BD•DC=AB2.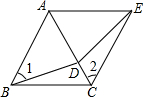 如图所示,点D为等边△ABC的AC边上的一点,∠1=∠2,BD=CE.求证:△DAE是等边三角形.
如图所示,点D为等边△ABC的AC边上的一点,∠1=∠2,BD=CE.求证:△DAE是等边三角形.