题目内容
用加减法解下列方程组:
(1)
(2)
(3)
(4)
.
(1)
|
(2)
|
(3)
|
(4)
|
考点:解二元一次方程组
专题:
分析:(1)先把两式相加求出u的值,再代入①求出t的值;
(2)先把两式相减求出a的值,再代入①求出b的值;
(3)先用加减消元法求出y的值,再把y的值代入①求出x的值;
(4)先把①化为不含分母的式子,再用加减消元法求出y的值,再得出x的值即可.
(2)先把两式相减求出a的值,再代入①求出b的值;
(3)先用加减消元法求出y的值,再把y的值代入①求出x的值;
(4)先把①化为不含分母的式子,再用加减消元法求出y的值,再得出x的值即可.
解答:解:(1)
,①+②得,9u=18,解得u=2,把u=2代入①得,6+2t=7,解得t=
,
故此方程组的解为:
;
(2)
,②-①得,a=1,把a=1代入①得,b=1,
故此方程组的解为
;
(3)
,①×2+②得,-9y=-9,解得y=1,把y=1代入①得,2x=2,解得x=1,
故此方程组的解为
;
(4)原方程组可化为
,①×2-②得,-7y=-7,解得y=1,把y=1代入①得,x=1,
故此方程组的解为
.
|
| 1 |
| 2 |
故此方程组的解为:
|
(2)
|
故此方程组的解为
|
(3)
|
故此方程组的解为
|
(4)原方程组可化为
|
故此方程组的解为
|
点评:本题考查的是解二元一次方程组,熟知解二元一次方程组的加减消元法和代入消元法是解答此题的关键.

练习册系列答案
相关题目
在同一平面内,两条直线的位置关系可能是( )
| A、相交或垂直 |
| B、垂直或平行 |
| C、平行或相交 |
| D、相交或垂直或平行 |
 如图,直线AB、CD相交于点O,FO⊥CD于点O,且∠EOF=∠DOB,求∠EOB的度数.
如图,直线AB、CD相交于点O,FO⊥CD于点O,且∠EOF=∠DOB,求∠EOB的度数.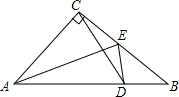 如图,已知在△ABC中,∠ACB=90°,AC=BC,AE是角平分线,ED⊥AB,垂足为D.求证:
如图,已知在△ABC中,∠ACB=90°,AC=BC,AE是角平分线,ED⊥AB,垂足为D.求证: