题目内容
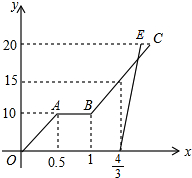 小张骑自行车,小李骑摩托车沿相同路线由甲地到乙地,小张先出发,骑行一段时间后因自行车出现故障进行维修,修好后按原来的速度继续骑行,小张离开甲地1小时20分后,小李开始骑行,如图是他们两人离开甲地的距离(千米)与(小时)之间的函数关系图象,已知小李的骑行速度是小张的3倍.
小张骑自行车,小李骑摩托车沿相同路线由甲地到乙地,小张先出发,骑行一段时间后因自行车出现故障进行维修,修好后按原来的速度继续骑行,小张离开甲地1小时20分后,小李开始骑行,如图是他们两人离开甲地的距离(千米)与(小时)之间的函数关系图象,已知小李的骑行速度是小张的3倍.解读信息:
(1)小张的骑行速度是
(2)图象中线段OA所在直线对应的函数关系式为
问题解决:
(1)分别求出线段BC、DE所在直线对应的函数关系式;
(2)小张骑行多少小时后被小李追上?此时小李骑行了多少千米?
考点:一次函数的应用
专题:
分析:(1)根据图象,小张骑行0.5小时时,骑行10千米,即可求得骑车的速度,根据图象求得修车的时间;
(2)利用待定系数法求得函数的解析式;
问题解决:
(1)首先根据速度和路程的关系求得C、E的坐标,利用待定系数法求得函数的解析式;
(2)求两个函数的解析式组成的方程组即可解决.
(2)利用待定系数法求得函数的解析式;
问题解决:
(1)首先根据速度和路程的关系求得C、E的坐标,利用待定系数法求得函数的解析式;
(2)求两个函数的解析式组成的方程组即可解决.
解答:解:(1)小张的骑行速度是:10÷0.5=20(千米/小时);
修车所用的时间是1-0.5=0.5(小时);
(2)设线段OA的解析式是y=kx,把(0.5,10)代入解析式得:k=20,则函数式是y=20x;
问题解决:
(1)甲骑车维修后到离出发地20千米,所用的时间是(20-10)÷20=0.5,
则C的坐标是(1.5,20).
设线段BC的解析式是y=kx+b,根据题意得:
,
解得:
,
则线段BC的解析式是:y=20x-10;
小李的速度是60千米/小时,则小李从出发到离出发地20千米所用的时间是
=
小时,
则E的坐标是(
,20),
设DE的解析式是y=mx+n,根据题意得:
,
解得:
,
则DE的解析式是y=60x-80;
(2)根据题意得:
,
解得:
,
则小张骑行
小时后被小李追上,此时小李骑行了25千米.
修车所用的时间是1-0.5=0.5(小时);
(2)设线段OA的解析式是y=kx,把(0.5,10)代入解析式得:k=20,则函数式是y=20x;
问题解决:
(1)甲骑车维修后到离出发地20千米,所用的时间是(20-10)÷20=0.5,
则C的坐标是(1.5,20).
设线段BC的解析式是y=kx+b,根据题意得:
|
解得:
|
则线段BC的解析式是:y=20x-10;
小李的速度是60千米/小时,则小李从出发到离出发地20千米所用的时间是
| 20 |
| 60 |
| 1 |
| 3 |
则E的坐标是(
| 5 |
| 3 |
设DE的解析式是y=mx+n,根据题意得:
|
解得:
|
则DE的解析式是y=60x-80;
(2)根据题意得:
|
解得:
|
则小张骑行
| 7 |
| 4 |
点评:本题考查的是用一次函数解决实际问题,关键是理解横纵坐标的意义,此类题是近年中考中的热点问题.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
已知x1=-1,x2=2是方程x2+mx+n=0的两根,则m的值是( )
| A、1 | B、-1 | C、2 | D、-1 |
 路边有两根相距4m的电线杆AB,CD,分别在高为3m的A处和高为6m的C处用铁丝将两电线杆固定
路边有两根相距4m的电线杆AB,CD,分别在高为3m的A处和高为6m的C处用铁丝将两电线杆固定 如图,直线AB、CD相交于点O,FO⊥CD于点O,且∠EOF=∠DOB,求∠EOB的度数.
如图,直线AB、CD相交于点O,FO⊥CD于点O,且∠EOF=∠DOB,求∠EOB的度数.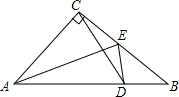 如图,已知在△ABC中,∠ACB=90°,AC=BC,AE是角平分线,ED⊥AB,垂足为D.求证:
如图,已知在△ABC中,∠ACB=90°,AC=BC,AE是角平分线,ED⊥AB,垂足为D.求证: