题目内容
将下面的抛物线向上平移3个单位，再向左平移2个单位后能得到抛物线y=3x2的是（ ）
| A、y=3（x+2）2+3 |
| B、y=3（x-2）2+3 |
| C、y=3（x+2）2-3 |
| D、y=3（x-2）2-3 |
考点：二次函数图象与几何变换
专题：几何变换
分析：逆向平移：抛物线y=3x2向下平移3个单位，再向右平移2个单位后得到的抛物线解析式为y=3（x-2）2-3，由此可对各选项进行判断．
解答：解：抛物线y=3x2的顶点坐标为（0，0），把点（0，0）向下平移3个单位，再向右平移2个单位后得到对应点的坐标为（2，-3），
所以把抛物线y=3x2向下平移3个单位，再向右平移2个单位后得到的抛物线解析式为y=3（x-2）2-3，
即把抛物线解析式y=3（x-2）2-3向上平移3个单位，再向左平移2个单位后能得到抛物线y=3x2．
故选D．
所以把抛物线y=3x2向下平移3个单位，再向右平移2个单位后得到的抛物线解析式为y=3（x-2）2-3，
即把抛物线解析式y=3（x-2）2-3向上平移3个单位，再向左平移2个单位后能得到抛物线y=3x2．
故选D．
点评：本题考查了二次函数图象与几何变换：由于抛物线平移后的形状不变，故a不变，所以求平移后的抛物线解析式通常可利用两种方法：一是求出原抛物线上任意两点平移后的坐标，利用待定系数法求出解析式；二是只考虑平移后的顶点坐标，即可求出解析式．
练习册系列答案
相关题目
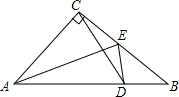如图，已知在△ABC中，∠ACB=90°，AC=BC，AE是角平分线，ED⊥AB，垂足为D．求证：
