题目内容
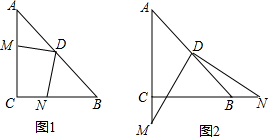 如图1,在△ABC中,CA=CB,∠ACB=90°,D为AB的中点,M,N分别为AC,BC上的点,且DM⊥DN.
如图1,在△ABC中,CA=CB,∠ACB=90°,D为AB的中点,M,N分别为AC,BC上的点,且DM⊥DN.(1)求证:CM+CN=
| 2 |
(2)如图2,若M,N分别在AC、CB的延长线上,探究CM、CN、BD之间的数量关系.
考点:全等三角形的判定与性质,等腰直角三角形
专题:
分析:(1)根据等腰直角三角形的性质和等腰直角三角形斜边上的中线性质得到∠A=∠B=∠ACD=∠DCB=45°,AC=BC,CD⊥AB,CD=BD=AD,再利用等角的余角相等得到∠CDM=∠BDN,然后根据“ASA”可判断△CMD≌△BDN,则CM=BN;
(2)根据等腰直角三角形的性质和等腰直角三角形斜边上的中线性质得到∠A=∠B=∠ACD=∠DCB=45°,AC=BC,CD⊥AB,CD=BD=AD,求出∠DCM=∠DBN=135°,然后根据“ASA”可判断△DCM≌△DBN,推出CM=BN即可.
(2)根据等腰直角三角形的性质和等腰直角三角形斜边上的中线性质得到∠A=∠B=∠ACD=∠DCB=45°,AC=BC,CD⊥AB,CD=BD=AD,求出∠DCM=∠DBN=135°,然后根据“ASA”可判断△DCM≌△DBN,推出CM=BN即可.
解答:证明:(1)如图1,连接CD,

∵△ACB是等腰直角三角形,D为斜边AB的中点,
∴∠A=∠B=∠ACD=∠DCB=45°,AC=BC,CD⊥AB,CD=BD=AD,
∴∠CDB=90°,
∵DM⊥DN,
∴∠MDN=90°,
∴∠MDC=∠BDN=90°-∠CDN,
在△CMD和△BND中,
,
∴△CMD≌△BND(ASA),
∴DM=BN,
在Rt△CDB中,∠CDB=90°,CD=BD,由勾股定理得:BC=
BD,
即CM+CN=BN+CN=BC=
BD;
(2)解:CN-CM=
BD,
理由是:如图2,连接CD,

∵△ACB是等腰直角三角形,D为斜边AB的中点,
∴∠A=∠B=∠ACD=∠DCB=45°,AC=BC,CD⊥AB,CD=BD=AD,
∴∠CDB=90°,∠DCM=∠DBN=135°,
∵DM⊥DN,
∴∠MDN=90°,
∴∠MDC=∠BDN=90°-∠CDN,
在△CMD和△BND中,
,
∴△CMD≌△BND(ASA),
∴DM=BN,
在Rt△CDB中,∠CDB=90°,CD=BD,由勾股定理得:BC=
BD,
即CN-CM=CN-BN=BC=
BD.

∵△ACB是等腰直角三角形,D为斜边AB的中点,
∴∠A=∠B=∠ACD=∠DCB=45°,AC=BC,CD⊥AB,CD=BD=AD,
∴∠CDB=90°,
∵DM⊥DN,
∴∠MDN=90°,
∴∠MDC=∠BDN=90°-∠CDN,
在△CMD和△BND中,
|
∴△CMD≌△BND(ASA),
∴DM=BN,
在Rt△CDB中,∠CDB=90°,CD=BD,由勾股定理得:BC=
| 2 |
即CM+CN=BN+CN=BC=
| 2 |
(2)解:CN-CM=
| 2 |
理由是:如图2,连接CD,

∵△ACB是等腰直角三角形,D为斜边AB的中点,
∴∠A=∠B=∠ACD=∠DCB=45°,AC=BC,CD⊥AB,CD=BD=AD,
∴∠CDB=90°,∠DCM=∠DBN=135°,
∵DM⊥DN,
∴∠MDN=90°,
∴∠MDC=∠BDN=90°-∠CDN,
在△CMD和△BND中,
|
∴△CMD≌△BND(ASA),
∴DM=BN,
在Rt△CDB中,∠CDB=90°,CD=BD,由勾股定理得:BC=
| 2 |
即CN-CM=CN-BN=BC=
| 2 |
点评:本题考查了全等三角形的性质和判定,等腰直角三角形的性质,勾股定理的应用,能推出△CMD≌△BND是解此题的关键,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,全等三角形的对应边相等,对应角相等.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目

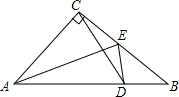 如图,已知在△ABC中,∠ACB=90°,AC=BC,AE是角平分线,ED⊥AB,垂足为D.求证:
如图,已知在△ABC中,∠ACB=90°,AC=BC,AE是角平分线,ED⊥AB,垂足为D.求证: 如图所示,AB是⊙O的切线,切点为B,AO交⊙O于点C,过C点的切线交AB于点D.若AD=3BD,CD=2,求⊙O的半径.
如图所示,AB是⊙O的切线,切点为B,AO交⊙O于点C,过C点的切线交AB于点D.若AD=3BD,CD=2,求⊙O的半径. 作出这段弧的圆心O.
作出这段弧的圆心O.