题目内容
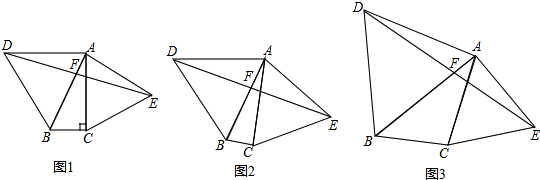
如图，PA、PB、CD分别与⊙O相切于A、B、E，若∠COD=50°，则∠P=（ ）| A、80° | B、55° |
| C、130° | D、65° |
考点：切线的性质,多边形内角与外角
专题：
分析：连接OA、OB、OP，由切线的性质得∠AOB=100°，再由四边形的内角和定理求得∠P的度数．
解答：
解：连接OA、OB、OP，
∵PA、PB、CD分别与⊙O相切，
∴AC=CE，ED=BD，OE⊥CD，
∴∠AOC=∠POC，∠BOD=∠POD，OA⊥PA，OB⊥PB，
∵∠COD=50°，
∴∠AOB=100°，
∴∠P=360°-∠AOB-∠PAO-∠PBO=360°-100°-90°-90°=80°．
故选A．
解：连接OA、OB、OP，∵PA、PB、CD分别与⊙O相切，
∴AC=CE，ED=BD，OE⊥CD，
∴∠AOC=∠POC，∠BOD=∠POD，OA⊥PA，OB⊥PB，
∵∠COD=50°，
∴∠AOB=100°，
∴∠P=360°-∠AOB-∠PAO-∠PBO=360°-100°-90°-90°=80°．
故选A．
点评：本题考查了切线的性质、切线长定理、四边形的内角和定理，是基础知识要熟练掌握．
练习册系列答案
相关题目
已知x1=-1，x2=2是方程x2+mx+n=0的两根，则m的值是（ ）
| A、1 | B、-1 | C、2 | D、-1 |
如图，直线AB、CD相交于点O，FO⊥CD于点O，且∠EOF=∠DOB，求∠EOB的度数．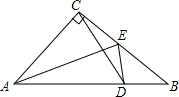
如图，已知在△ABC中，∠ACB=90°，AC=BC，AE是角平分线，ED⊥AB，垂足为D．求证：
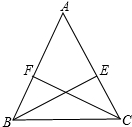已知在△ABC中，AB=AC，CF⊥AB于F，BE⊥AC于E，求证：AE=AF．