题目内容
19. 已知:如图△ABC中,AD⊥BC,CE⊥AB,垂足分别是D、E,AD和CE相交于O,且AD=CD.求证:BD=OD.
已知:如图△ABC中,AD⊥BC,CE⊥AB,垂足分别是D、E,AD和CE相交于O,且AD=CD.求证:BD=OD.
分析 由AAS证明△ABD≌△COD,然后由全等三角形的性质,证得结论.
解答 证明:∵AD⊥BC,CE⊥AB,
∴∠ADB=∠CDO=∠CEB=90°,
∴∠BAD+∠B=∠OCD+∠B=90°,
∴∠BAD=∠OCD,
在△ABD和△COD中,$\left\{\begin{array}{l}{∠ADB=∠CD}&{\;}\\{∠BAD=∠OCD}&{\;}\\{AD=CD}&{\;}\end{array}\right.$,
∴△ABD≌△COD(AAS),
∴BD=OD.
点评 此题考查了全等三角形的判定与性质的应用,证明三角形全等是解决问题的关键,注意掌握数形结合思想的应用.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
14.如图图案是晋商大院窗格的一部分,其中“○”代表窗纸上所贴的剪纸,则第8个图中所贴剪纸“○”的个数为( )
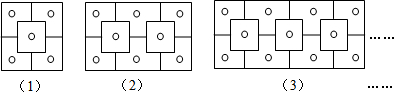

| A. | 23个 | B. | 24个 | C. | 25个 | D. | 26个 |
 如图,AB与CD相交于点O,△OBD∽△OAC,$\frac{OD}{OC}$=$\frac{2}{3}$,OB=4,求AO和AB的长.
如图,AB与CD相交于点O,△OBD∽△OAC,$\frac{OD}{OC}$=$\frac{2}{3}$,OB=4,求AO和AB的长. 如图,已知AB∥CD,O为∠CAB、∠ACD的角平分线的交点,OE⊥AC于E,且OE=2,则两平行线间AB、CD的距离等于4.
如图,已知AB∥CD,O为∠CAB、∠ACD的角平分线的交点,OE⊥AC于E,且OE=2,则两平行线间AB、CD的距离等于4. 如图,点C、B、E在同一条直线上,AB∥DE,∠ACB=∠CDE,AC=CD,求证:AB=CE.
如图,点C、B、E在同一条直线上,AB∥DE,∠ACB=∠CDE,AC=CD,求证:AB=CE.