题目内容
6.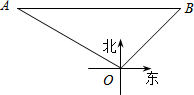 在海上某固定观测点O处的北偏西60°方向,且距离O处40海里的A处,有一艘货轮正沿着正东方向匀速航行,2小时后,此货轮到达O处的北偏东45°方向的B处.在该货轮从A处到B处的航行过程中.
在海上某固定观测点O处的北偏西60°方向,且距离O处40海里的A处,有一艘货轮正沿着正东方向匀速航行,2小时后,此货轮到达O处的北偏东45°方向的B处.在该货轮从A处到B处的航行过程中.(1)求货轮离观测点O处的最短距离;
(2)求货轮的航速.
分析 (1)如图,作OH⊥AB,垂足为H.通过解Rt△AOH来求OH的长度即可;
(2)在Rt△AOH中,求得AH的长度;然后在Rt△BOH中,∠B=∠HOB=45°,则△BHO的等腰直角三角形,故HB=HO=20.易求AB=20$\sqrt{3}$+20,利用速度=路程÷时间进行计算.
解答 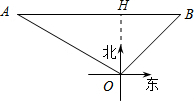 解:(1)如图,作OH⊥AB,垂足为H.
解:(1)如图,作OH⊥AB,垂足为H.
在Rt△AOH中,∵cos∠AOH=$\frac{OH}{AO}$.
∴OH=cos60°•AO=20.
即货轮离观测点O处的最短距离为20海里;
(2)在Rt△AOH中,∵sin∠AOH=$\frac{AH}{AO}$,
∴AH=sin60°•AO=20$\sqrt{3}$,
在Rt△BOH中,∵∠B=∠HOB=45°,
∴HB=HO=20.
∴AB=20$\sqrt{3}$+20,
∴货轮的航速为$\frac{20\sqrt{3}+20}{2}$=10$\sqrt{3}$+10(海里/小时).
点评 本题考查了解直角三角形的应用,难度适中.解一般三角形,求三角形的边或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.

练习册系列答案
相关题目
16.在平面直角坐标系中,点($\sqrt{3}$,1)绕原点顺时针旋转60°后得到点( )
| A. | ($\sqrt{3}$,-1) | B. | (-1,$\sqrt{3}$) | C. | (-$\sqrt{3}$,1) | D. | (1,-$\sqrt{3}$) |
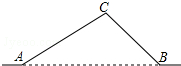 如图,从城市A到B城市的公路需经过城市C,图中AC=100千米,∠CAB=25°,∠CBA=37°,因城市规划的需要,将在A、B两城市间修建一条笔直的公路.
如图,从城市A到B城市的公路需经过城市C,图中AC=100千米,∠CAB=25°,∠CBA=37°,因城市规划的需要,将在A、B两城市间修建一条笔直的公路. 如图,已知AB是⊙O的直径,C是⊙O上一点,∠BAC的平分线交⊙O于点D,交⊙O的切线BE于点E,过点D作DF⊥AC,交AC的延长线于点F.
如图,已知AB是⊙O的直径,C是⊙O上一点,∠BAC的平分线交⊙O于点D,交⊙O的切线BE于点E,过点D作DF⊥AC,交AC的延长线于点F.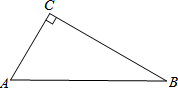 在Rt△ABC中,∠ACB=90°.
在Rt△ABC中,∠ACB=90°. 如图是由6个相同的小正方体组成的几何体,那么这个几何体的俯视图是( )
如图是由6个相同的小正方体组成的几何体,那么这个几何体的俯视图是( )


