题目内容
17.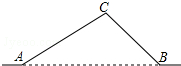 如图,从城市A到B城市的公路需经过城市C,图中AC=100千米,∠CAB=25°,∠CBA=37°,因城市规划的需要,将在A、B两城市间修建一条笔直的公路.
如图,从城市A到B城市的公路需经过城市C,图中AC=100千米,∠CAB=25°,∠CBA=37°,因城市规划的需要,将在A、B两城市间修建一条笔直的公路.(1)求改直的公路AB的长;
(2)问公路改直后比原来缩短了多少千米?
(参考数据:sin25°≈0.42,cos25°≈0.91,sin37°≈0.60,tan37°≈0.75)
分析 (1)作CH⊥AB于H.在Rt△ACH中根据CH=AC•sin∠CAB求出CH的长,由AH=AC•cos∠CAB求出AH的长,同理可得出BH的长,根据AB=AH+BH可得出结论;
(2)根据在Rt△BCH中,BC=CH÷sin∠CBA可得出BC的长,由AC+BC-AB即可得出结论.
解答  解:(1)作CH⊥AB于H.
解:(1)作CH⊥AB于H.
在Rt△ACH中,∵AC=100千米,∠CAB=25°,
∴CH=AC•sin∠CAB=AC•sin25°≈100×0.42=42千米,
AH=AC•cos∠CAB=AC•cos25°≈100×0.91=91千米.
在Rt△BCH中,∵∠CBA=37°,
∴BH=CH÷tan∠CBA=4.2÷tan37°≈42÷0.75=56千米,
∴AB=AH+BH=91+56=147千米.故改直的公路AB的长147千米;
(2)在Rt△BCH中,BC=CH÷sin∠CBA=42÷sin37°≈42÷0.6=70千米,
则AC+BC-AB=100+70-147=23千米.
答:公路改直后比原来缩短了23千米.
点评 本题考查的是解直角三角形的应用,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
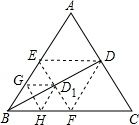 如图,△ABC是边长为1的等边三角形,BD为AC边上的高,将△ABC折叠,使点B与点D重合,折痕EF交BD于点D1,再将△BEF折叠,使点B于点D1重合,折痕GH交BD1于点D2,依次折叠,则BDn=$\frac{\sqrt{3}}{{2}^{n+1}}$.
如图,△ABC是边长为1的等边三角形,BD为AC边上的高,将△ABC折叠,使点B与点D重合,折痕EF交BD于点D1,再将△BEF折叠,使点B于点D1重合,折痕GH交BD1于点D2,依次折叠,则BDn=$\frac{\sqrt{3}}{{2}^{n+1}}$.
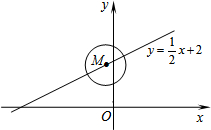 ⊙M的圆心在一次函数y=$\frac{1}{2}$x+2图象上,半径为1.当⊙M与y轴相切时,点M的坐标为(1,$\frac{5}{2}$)或(-1,$\frac{3}{2}$).
⊙M的圆心在一次函数y=$\frac{1}{2}$x+2图象上,半径为1.当⊙M与y轴相切时,点M的坐标为(1,$\frac{5}{2}$)或(-1,$\frac{3}{2}$).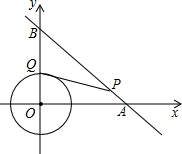 如图,⊙O是以原点为圆心,$\sqrt{2}$为半径的圆,点P是直线y=-x+6上的一点,过点P 作⊙O的一条切线PQ,Q为切点,则△OPQ面积的最小值为2$\sqrt{2}$.
如图,⊙O是以原点为圆心,$\sqrt{2}$为半径的圆,点P是直线y=-x+6上的一点,过点P 作⊙O的一条切线PQ,Q为切点,则△OPQ面积的最小值为2$\sqrt{2}$.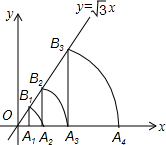 如图,已知直线y=$\sqrt{3}$x,点A1的坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以原点O为圆心,OB1的长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2的长为半径画弧交x轴于点A3,…,按此做法进行下去,则点B6的坐标为(32,32$\sqrt{3}$).
如图,已知直线y=$\sqrt{3}$x,点A1的坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以原点O为圆心,OB1的长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2的长为半径画弧交x轴于点A3,…,按此做法进行下去,则点B6的坐标为(32,32$\sqrt{3}$).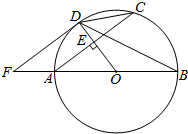 如图,AB是⊙O的直径.半径OD垂直弦AC于点E.F是BA延长线上一点,∠CDB=∠BFD.
如图,AB是⊙O的直径.半径OD垂直弦AC于点E.F是BA延长线上一点,∠CDB=∠BFD.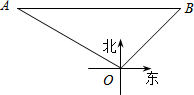 在海上某固定观测点O处的北偏西60°方向,且距离O处40海里的A处,有一艘货轮正沿着正东方向匀速航行,2小时后,此货轮到达O处的北偏东45°方向的B处.在该货轮从A处到B处的航行过程中.
在海上某固定观测点O处的北偏西60°方向,且距离O处40海里的A处,有一艘货轮正沿着正东方向匀速航行,2小时后,此货轮到达O处的北偏东45°方向的B处.在该货轮从A处到B处的航行过程中.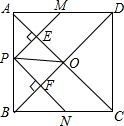 如图,在正方形ABCD中,点P是AB边上一动点(不与A、B重合),对角线AC、BD相交于点O,过点P分别作AC、BD的垂线,分别交AC、BD于点E、F,交AD、BC于点M、N.下列结论:①△APE≌△AME;②PM+PN=AC;③PE2+PF2=PO2;④△POF∽△BNF.其中正确的结论有3个.
如图,在正方形ABCD中,点P是AB边上一动点(不与A、B重合),对角线AC、BD相交于点O,过点P分别作AC、BD的垂线,分别交AC、BD于点E、F,交AD、BC于点M、N.下列结论:①△APE≌△AME;②PM+PN=AC;③PE2+PF2=PO2;④△POF∽△BNF.其中正确的结论有3个.