题目内容
14.函数y=2x2-7x+3顶点坐标为($\frac{7}{4}$,-$\frac{25}{8}$).分析 利用顶点坐标公式(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$),直接求解.
解答 解:∵x=-$\frac{b}{2a}$=-$\frac{-7}{2×2}$=$\frac{7}{4}$,y=$\frac{4ac-{b}^{2}}{4a}$=$\frac{4×2×3-{7}^{2}}{4×2}$=-$\frac{25}{8}$,
∴顶点坐标是($\frac{7}{4}$,-$\frac{25}{8}$).
故答案为($\frac{7}{4}$,-$\frac{25}{8}$).
点评 本题考查了二次函数的性质,熟练运用顶点公式求抛物线的顶点坐标.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
3.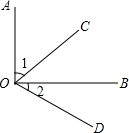 如图,如果∠AOB=∠COD=90°,那么∠1=∠2,这是根据( )
如图,如果∠AOB=∠COD=90°,那么∠1=∠2,这是根据( )
 如图,如果∠AOB=∠COD=90°,那么∠1=∠2,这是根据( )
如图,如果∠AOB=∠COD=90°,那么∠1=∠2,这是根据( )| A. | 直角都相等 | B. | 等角的余角相等 | C. | 同角的余角相等 | D. | 同角的补角相等 |
4.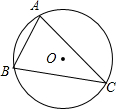 ⊙O是△ABC的外接圆,⊙O的半径R=2,sinB=$\frac{3}{4}$,则弦AC的长为( )
⊙O是△ABC的外接圆,⊙O的半径R=2,sinB=$\frac{3}{4}$,则弦AC的长为( )
 ⊙O是△ABC的外接圆,⊙O的半径R=2,sinB=$\frac{3}{4}$,则弦AC的长为( )
⊙O是△ABC的外接圆,⊙O的半径R=2,sinB=$\frac{3}{4}$,则弦AC的长为( )| A. | $\frac{1}{2}$ | B. | 1 | C. | 3 | D. | $\frac{\sqrt{3}}{2}$ |
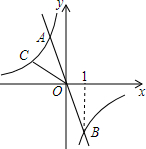 已知:如图,一次函数y1=-2x的图象与反比例函数${y_2}=\frac{k}{x}$的图象交于A、B两点,且点B的坐标为(1,m).
已知:如图,一次函数y1=-2x的图象与反比例函数${y_2}=\frac{k}{x}$的图象交于A、B两点,且点B的坐标为(1,m).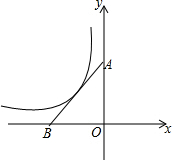 如图,在平面直角坐标系中,点A,B分别在y轴的正半轴和x轴的负半轴上,Rt△AOB的面积是4,若反比例函数y=$\frac{k}{x}$在第二象限内的图象经过斜边AB的中点,则k的值是-2.
如图,在平面直角坐标系中,点A,B分别在y轴的正半轴和x轴的负半轴上,Rt△AOB的面积是4,若反比例函数y=$\frac{k}{x}$在第二象限内的图象经过斜边AB的中点,则k的值是-2.