题目内容
6．
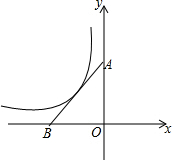如图，在平面直角坐标系中，点A，B分别在y轴的正半轴和x轴的负半轴上，Rt△AOB的面积是4，若反比例函数y=$\frac{k}{x}$在第二象限内的图象经过斜边AB的中点，则k的值是-2．
分析 设斜边AB的中点坐标为（x，y），则A（0，2y），B（2x，0），根据三角形的面积公式得出关于xy的方程，求得xy的值，就是k的值．
解答 解：设斜边AB的中点坐标为（x，y），则A（0，2y），B（2x，0），
∵S△AOB=$\frac{1}{2}$OA•OB=4，
∴$\frac{1}{2}$×（-2x）×2y=4，
∴xy=-2，
∵反比例函数y=$\frac{k}{x}$在第二象限内的图象经过斜边AB的中点，
∴k=xy=-2，
故答案为-2．
点评 本题考查了反比例函数图象上点的坐标特征，图象上的点的坐标符合解析式．
练习册系列答案
相关题目
17．
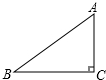如图，在Rt△ABC中，∠C=90°，AC=3，AB=5．则sinB等于（ ）
如图，在Rt△ABC中，∠C=90°，AC=3，AB=5．则sinB等于（ ）| A． | $\frac{3}{5}$ | B． | $\frac{4}{5}$ | C． | $\frac{3}{4}$ | D． | $\frac{4}{3}$ |
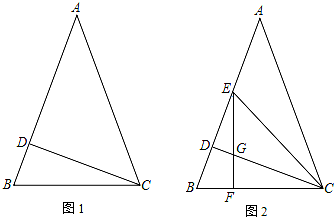
如图，在△ABC中，点D在AC上，且BD=BC=AD，∠DBC=20度，求∠A、∠C，∠ABC的度数．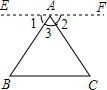
已知△ABC，求证∠A+∠B+∠C=180°．请在括号里填上适当的理由．