题目内容
2.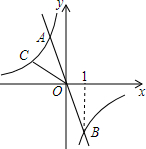 已知:如图,一次函数y1=-2x的图象与反比例函数${y_2}=\frac{k}{x}$的图象交于A、B两点,且点B的坐标为(1,m).
已知:如图,一次函数y1=-2x的图象与反比例函数${y_2}=\frac{k}{x}$的图象交于A、B两点,且点B的坐标为(1,m).(1)求反比例函数的表达式;
(2)点C(n,1)在反比例函数AB⊥CD的图象上,求△AOC的面积;
(3)求使得y1≤y2成立的x取值范围.
分析 (1)把点B坐标代入一次函数y1=-2x,得出m的值,再把点B坐标代入反比例函数${y_2}=\frac{k}{x}$即可得出k的值,从而得出反比例函数的表达式;
(2)将点C(n,1)在反比例函数解析式即可得出n的值,S△AOC=S四边形ACFE-S△AOE,从而得出△AOC的面积;
(3)由图象直接得出y1≤y2成立的x取值范围.
解答 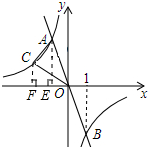 解:(1)把点B坐标代入一次函数y1=-2x,
解:(1)把点B坐标代入一次函数y1=-2x,
得m=-2,
∴B(1,-2),
把点B坐标代入反比例函数${y_2}=\frac{k}{x}$,得k=-2,
∴反比例函数的表达式y2=-$\frac{2}{x}$;
(2)过点A作AE⊥x轴,CF⊥x轴,
将点C(n,1)在反比例函数解析式,得n=-2,
∴S△AOC=S四边形ACFE+S△AOE-S△COF=$\frac{1+2}{2}$+1-1=$\frac{3}{2}$,
∴△AOC的面积为$\frac{3}{2}$;
(3)由图象直接得出y1≤y2成立的x取值范围是-1≤x<0或x≥1.
点评 本题考查了一次函数与反比例函数的交点问题,用待定系数法求一次函数的解析式等知识点,主要考查学生的计算能力和观察图形的能力,用了数形结合思想.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
10. 如图所示,该几何体的俯视图是( )
如图所示,该几何体的俯视图是( )
 如图所示,该几何体的俯视图是( )
如图所示,该几何体的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
17.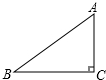 如图,在Rt△ABC中,∠C=90°,AC=3,AB=5.则sinB等于( )
如图,在Rt△ABC中,∠C=90°,AC=3,AB=5.则sinB等于( )
 如图,在Rt△ABC中,∠C=90°,AC=3,AB=5.则sinB等于( )
如图,在Rt△ABC中,∠C=90°,AC=3,AB=5.则sinB等于( )| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
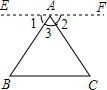 已知△ABC,求证∠A+∠B+∠C=180°.请在括号里填上适当的理由.
已知△ABC,求证∠A+∠B+∠C=180°.请在括号里填上适当的理由.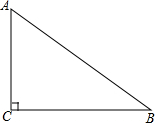 如图,在Rt△ABC中,∠C=90°,sinB=$\frac{3}{5}$,BC=5cm,以点C为圆心,以3cm的长为半径作圆,则⊙C与AB的位置关系是( )
如图,在Rt△ABC中,∠C=90°,sinB=$\frac{3}{5}$,BC=5cm,以点C为圆心,以3cm的长为半径作圆,则⊙C与AB的位置关系是( )