题目内容
5.观察下列等式:阅读下列材料:
1×2=$\frac{1}{3}$(1×2×3-0×1×2),
2×3=$\frac{1}{3}$(2×3×4-1×2×3),
3×4=$\frac{1}{3}$(3×4×5-2×3×4),
由以上三个等式相加,可得1×2+2×3+3×4=$\frac{1}{3}$×3×4×5=20
读完以上材料,请你计算下列各题,其中(1)需要写出过程,其它试题直接写出答案.
(1)1×2+2×3+3×4+…+6×7;
(2)1×2+2×3+3×4+…+n×(n+1)=$\frac{1}{3}$n(n+1)(n+2);
(3)1×2+2×3+3×4+3×4×5+…+6×7×8=746;
(4)1×2+2×3+3×4+3×4×5+…+n×(n+1)×(n+2)=$\frac{1}{4}$n(n+1)(n+2)(n+3)-10.
分析 (1)根据题目信息列出算式,然后提取$\frac{1}{3}$,进行计算即可得解;
(2)观察不难发现,两个连续的自然数的积等于这两个数与后面的数的积减去与前面的数的积的$\frac{1}{3}$,然后列出算式进行计算即可得解;
(3)1×2+2×3+3×4根据(2)的规律列式进行计算,3×4×5+…+6×7×8可补上1×2×3+2×3×4,然后类比(2)中结论计算,再减去之前补上的1×2×3+2×3×4,总体列式计算可得;
(4)类比(3)中相同做法列式计算.
解答 解:(1)1×2+2×3+3×4+…+10×11,
=$\frac{1}{3}$×(1×2×3-0×1×2)+$\frac{1}{3}$×(2×3×4-1×2×3)+$\frac{1}{3}$×(3×4×5-2×3×4)+…+$\frac{1}{3}$×(6×7×8-5×6×7),
=$\frac{1}{3}$×(1×2×3-0×1×2+2×3×4-1×2×3+3×4×5-2×3×4+…+6×7×8-5×6×7),
=$\frac{1}{3}$×6×7×8,
=112;
(2)∵1×2+2×3+3×4=$\frac{1}{3}$×3×4×5,
∴1×2+2×3+3×4+…+n×(n+1)=$\frac{1}{3}$n(n+1)(n+2);
(3)1×2+2×3+3×4+3×4×5+…+6×7×8
=$\frac{1}{3}$×3×4×5+$\frac{1}{4}$×6×7×8×9-$\frac{1}{4}$×2×3×4×5
=20+756-30
=746;
(4)1×2+2×3+3×4+3×4×5+…+n×(n+1)×(n+2)
=$\frac{1}{3}$×3×4×5+$\frac{1}{4}$×n×(n+1)×(n+2)×(n+3)-$\frac{1}{4}$×2×3×4×5
=$\frac{1}{4}$n(n+1)(n+2)(n+3)-10.
点评 本题是对数字变化规律的考查,难度较大,利用类比的思想求解即可,观察出(2)的变化规律是解题的关键.

| A. | y=-3x | B. | y=4x-1 | C. | y=$\frac{6}{x}$ | D. | y=x2-2x+1 |
| A. | 8-3+5-7 | B. | 3+8-7-5 | C. | -5-7-3+8 | D. | 8+3-5+7 |
 如图所示,该几何体的俯视图是( )
如图所示,该几何体的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
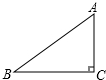 如图,在Rt△ABC中,∠C=90°,AC=3,AB=5.则sinB等于( )
如图,在Rt△ABC中,∠C=90°,AC=3,AB=5.则sinB等于( )| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |