题目内容
18. 在平面直角坐标系中,直线y=-x+2与反比例函数y=$\frac{1}{x}$的图象有唯一公共点,若直线y=-x+b与反比例函数y=$\frac{1}{x}$的图象有2个公共点,则b的取值范围是b>2或b<-2.
在平面直角坐标系中,直线y=-x+2与反比例函数y=$\frac{1}{x}$的图象有唯一公共点,若直线y=-x+b与反比例函数y=$\frac{1}{x}$的图象有2个公共点,则b的取值范围是b>2或b<-2.
分析 联立两函数解析式消去y可得x2-bx+1=0,由直线y=-x+b与反比例函数y=$\frac{1}{x}$的图象有2个公共点,得到方程x2-bx+1=0有两个不相等的实数根,根据根的判别式可得结果.
解答 解:解方程组$\left\{\begin{array}{l}{y=-x+b}\\{y=\frac{1}{x}}\end{array}\right.$得:x2-bx+1=0,
∵直线y=-x+b与反比例函数y=$\frac{1}{x}$的图象有2个公共点,
∴方程x2-bx+1=0有两个不相等的实数根,
∴△=b2-4>0,
∴b>2或b<-2,
故答案为b>2或b<-2.
点评 本题主要考查函数的交点问题,把两函数图象的交点问题转化成一元二次方程根的问题是解题的关键.

练习册系列答案
相关题目
8.下列多项式乘法,能用平方差公式计算的是( )
| A. | (-3x-2)(3x+2) | B. | (-a-b)(-b+a) | C. | (-3x+2)(2-3x) | D. | (3x+2)(2x-3) |
9.某件商品,按成本价提高40%后标价,又以8折优惠卖出,结果仍可获利15元,则这件商品的成本价为( )
| A. | 115元 | B. | 120元 | C. | 125元 | D. | 150元 |
7. 如图,表示$\sqrt{8}$的点在数轴上表示时,所在哪两个字母之间( )
如图,表示$\sqrt{8}$的点在数轴上表示时,所在哪两个字母之间( )
 如图,表示$\sqrt{8}$的点在数轴上表示时,所在哪两个字母之间( )
如图,表示$\sqrt{8}$的点在数轴上表示时,所在哪两个字母之间( )| A. | C与D | B. | A与B | C. | A与C | D. | B与C |
 一、阅读理解:
一、阅读理解: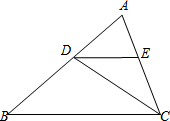 如图所示,已知△ABC中,AB=2,D在AB边上移动(不与A、B重合),DE∥BC交AC于E,连CD.设S△ABC=S,S△DEC=S1.
如图所示,已知△ABC中,AB=2,D在AB边上移动(不与A、B重合),DE∥BC交AC于E,连CD.设S△ABC=S,S△DEC=S1.