题目内容
5.解方程:$\frac{x}{x-1}+\frac{5x+12}{{{x^2}-x}}$=1.分析 分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:去分母得:x2+5x+12=x2-x,
解得:x=-2,
经检验x=-2是分式方程的解.
点评 此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
20.下列因式分解中,正确的是( )
| A. | m2-n2=(m-n)2 | B. | 3x2-x=x(3x-1) | ||
| C. | x4-2x2y2+y4=(x2-y2)2 | D. | x2-3x-4=(x+4)(x-1) |
10.在△ABC中,∠C=90°,若AC=3,BC=5,则AB等于( )
| A. | $\sqrt{34}$ | B. | 4 | C. | $\sqrt{20}$ | D. | 都不对 |
15.若一直角三角形两边长为4和5,则第三边长为( )
| A. | 3 | B. | $\sqrt{41}$ | C. | 3或$\sqrt{41}$ | D. | 不确定 |
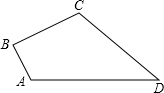 如图,在四边形ABCD中,AB=1,BC=$\sqrt{2}$,CD=5,AD=2$\sqrt{7}$,∠B=90°,求四边形ABCD的面积.
如图,在四边形ABCD中,AB=1,BC=$\sqrt{2}$,CD=5,AD=2$\sqrt{7}$,∠B=90°,求四边形ABCD的面积.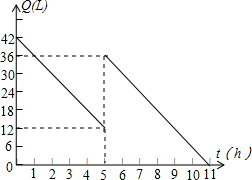 某机动车出发前油箱内有油42L,行驶若干小时后,在途中加油站加油若干升.油箱中余油量Q(L)与行驶时间t(h)之间的函数关系如图所示,根据如图回答问题:
某机动车出发前油箱内有油42L,行驶若干小时后,在途中加油站加油若干升.油箱中余油量Q(L)与行驶时间t(h)之间的函数关系如图所示,根据如图回答问题: