题目内容
14.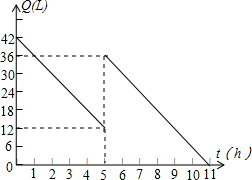 某机动车出发前油箱内有油42L,行驶若干小时后,在途中加油站加油若干升.油箱中余油量Q(L)与行驶时间t(h)之间的函数关系如图所示,根据如图回答问题:
某机动车出发前油箱内有油42L,行驶若干小时后,在途中加油站加油若干升.油箱中余油量Q(L)与行驶时间t(h)之间的函数关系如图所示,根据如图回答问题:(1)机动车行驶几小时后加油?加了多少油?
(2)试求加油前油箱余油量Q与行驶时间t之间的关系式;
(3)如果加油站离目的地还有230km,车速为40km/h,要到达目的地,油箱中的油是否够用?请说明理由.
分析 (1)根据函数图象的横坐标,可得答案;根据函数图象的纵坐标,可得加油量;
(2)根据待定系数法,可得函数解析式;
(3)根据单位耗油量乘以行驶时间,可得行驶路程,根据有理数的大小比较,可得答案.
解答 解:(1)由横坐标看出,5小时后加油,由纵坐标看出,加了36-12=24(L)油
(2)设解析式为Q=kt+b,将(0,42),(5,12)代入函数解析式,得
$\left\{\begin{array}{l}{b=42}\\{5t+b=12}\end{array}\right.$,
解得$\left\{\begin{array}{l}{t=-6}\\{b=42}\end{array}\right.$.
故函数解析式为Q=42-6t
(3)够用,理由如下
单位耗油量为$\frac{36}{6}$=6,
6×40-230=240-230=10>0,
还可以再行驶10千米,
故油够用.
点评 本题考查了函数图象,观察函数图象的横坐标得出时间,观察函数图象的纵坐标得出剩余油量是解题关键,利用待定系数法求函数解析式.

练习册系列答案
相关题目
4.若点p(a,b)在第一象限,则点Q(2a,-b)在( )
| A. | 第四象限 | B. | 第三象限 | C. | 第二象限 | D. | 第一象限 |
6.当算式-3-$\sqrt{a+b}$取最大值时,a,b的关系是( )
| A. | a和b相等 | B. | a和b互为相反数 | C. | a和b同号 | D. | 不存在 |