题目内容
15.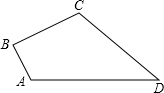 如图,在四边形ABCD中,AB=1,BC=$\sqrt{2}$,CD=5,AD=2$\sqrt{7}$,∠B=90°,求四边形ABCD的面积.
如图,在四边形ABCD中,AB=1,BC=$\sqrt{2}$,CD=5,AD=2$\sqrt{7}$,∠B=90°,求四边形ABCD的面积.
分析 连接AC,先根据勾股定理求出AC的长,再由勾股定理的逆定理判断出△ACD的形状,由S四边形ABCD=S△ABC+S△ACD即可得出结论.
解答 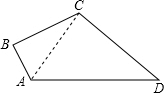 解:连接AC,
解:连接AC,
∵AB=1,BC=$\sqrt{2}$,∠B=90°,
∴AC=$\sqrt{{AB}^{2}+{BC}^{2}}$=$\sqrt{{1}^{2}+{(\sqrt{2})}^{2}}$=$\sqrt{3}$.
∵CD=5,AD=2$\sqrt{7}$,($\sqrt{3}$)2+52=(2$\sqrt{7}$)2,即AC2+CD2=AD2,
∴△ACD是直角三角形,
∴S四边形ABCD=S△ABC+S△ACD
=$\frac{1}{2}$AB•BC+$\frac{1}{2}$AC•CD
=$\frac{1}{2}$×1×$\sqrt{2}$+$\frac{1}{2}$×$\sqrt{3}$×5
=$\frac{\sqrt{2}}{2}$+$\frac{5\sqrt{3}}{2}$
=$\frac{\sqrt{2}+5\sqrt{3}}{2}$.
点评 本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
4.若点p(a,b)在第一象限,则点Q(2a,-b)在( )
| A. | 第四象限 | B. | 第三象限 | C. | 第二象限 | D. | 第一象限 |
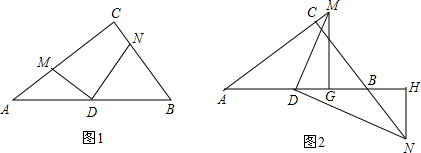
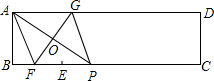 如图,矩形ABCD中,AD=7,AB=BE=2,点P是EC(包括E、C)上的动点,线段AP的垂直平分线分别交BC、AD于点F、G,设BP=x,AG=y.
如图,矩形ABCD中,AD=7,AB=BE=2,点P是EC(包括E、C)上的动点,线段AP的垂直平分线分别交BC、AD于点F、G,设BP=x,AG=y. 如图,以点B为顶点,射线BC为一边,利用尺规作∠EBC,使得∠EBC=∠A.
如图,以点B为顶点,射线BC为一边,利用尺规作∠EBC,使得∠EBC=∠A.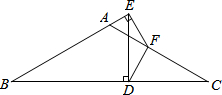 如图,△ABC中,AB=AC=2,∠B=30°,点D在BC上,过点D作DE⊥BC,交BA或其延长线于点E,过点E作EF⊥BA交AC或其延长线于点F,连接DF.若DF⊥AC,则BD=$\frac{6\sqrt{3}}{5}$.
如图,△ABC中,AB=AC=2,∠B=30°,点D在BC上,过点D作DE⊥BC,交BA或其延长线于点E,过点E作EF⊥BA交AC或其延长线于点F,连接DF.若DF⊥AC,则BD=$\frac{6\sqrt{3}}{5}$.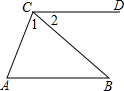 已知:如图,AB∥CD,∠B=35°,∠1=75°.求∠A的度数.
已知:如图,AB∥CD,∠B=35°,∠1=75°.求∠A的度数.