题目内容
14.计算下列各题:(1)$\sqrt{27}$-$\sqrt{\frac{1}{5}}$-($\sqrt{20}$-2$\sqrt{75}$);
(2)$\frac{{a}^{2}+1}{a-1}$-a+1.
分析 (1)先把各根式化为最减二次根式,再合并同类项即可;
(2)根据分式的加减法则进行计算即可.
解答 解:(1)原式=3$\sqrt{3}$-$\frac{\sqrt{5}}{5}$-(2$\sqrt{5}$-10$\sqrt{3}$)
=3$\sqrt{3}$-$\frac{\sqrt{5}}{5}$-2$\sqrt{5}$+10$\sqrt{3}$
=13$\sqrt{3}$-$\frac{5\sqrt{5}}{2}$;
(2)原式=$\frac{{a}^{2}+1}{a-1}$-$\frac{{a}^{2}-2a+1}{a-1}$
=$\frac{{a}^{2}+1-{a}^{2}+2a-1}{a-1}$
=$\frac{2a}{a-1}$.
点评 本题考查的是二次根式的加减法,熟知二次根式相加减,先把各个二次根式化成最简二次根式,再把被开方数相同的二次根式进行合并,合并方法为系数相加减,根式不变是解答此题的关键.

练习册系列答案
相关题目
19.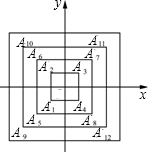 如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行.从内到外,它们的边长依次为2,4,6,8,10,…,顶点A1,A2,A3,A4,A5,A6…的坐标分别为A1(-1,-1),A2(-1,1),A3(1,1),A4(1,-1),A5(-2,-2),A6(-2,2),…,则顶点A55的坐标是( )
如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行.从内到外,它们的边长依次为2,4,6,8,10,…,顶点A1,A2,A3,A4,A5,A6…的坐标分别为A1(-1,-1),A2(-1,1),A3(1,1),A4(1,-1),A5(-2,-2),A6(-2,2),…,则顶点A55的坐标是( )
 如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行.从内到外,它们的边长依次为2,4,6,8,10,…,顶点A1,A2,A3,A4,A5,A6…的坐标分别为A1(-1,-1),A2(-1,1),A3(1,1),A4(1,-1),A5(-2,-2),A6(-2,2),…,则顶点A55的坐标是( )
如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行.从内到外,它们的边长依次为2,4,6,8,10,…,顶点A1,A2,A3,A4,A5,A6…的坐标分别为A1(-1,-1),A2(-1,1),A3(1,1),A4(1,-1),A5(-2,-2),A6(-2,2),…,则顶点A55的坐标是( )| A. | (13,13) | B. | (-13,-13) | C. | (-14,-14) | D. | (14,14) |
4.下列计算正确的是( )
| A. | 2a+a2=3a2 | B. | 5a2-2a2=3 | C. | (a3)2=a5 | D. | a2•a2=a4 |
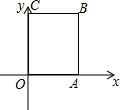 如图建立平面直角坐标系,长方形OABC中A(8,0),点C(0,10),点P从原点出发,以每秒1个单位长度的速度沿着O-C-B-A-O的路线运动到点O停止,设点P运动时间为t秒.
如图建立平面直角坐标系,长方形OABC中A(8,0),点C(0,10),点P从原点出发,以每秒1个单位长度的速度沿着O-C-B-A-O的路线运动到点O停止,设点P运动时间为t秒.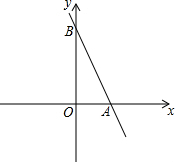 已知直线y=-2x+6与x轴交于点A,与y轴交于点B.
已知直线y=-2x+6与x轴交于点A,与y轴交于点B.