题目内容
6.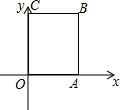 如图建立平面直角坐标系,长方形OABC中A(8,0),点C(0,10),点P从原点出发,以每秒1个单位长度的速度沿着O-C-B-A-O的路线运动到点O停止,设点P运动时间为t秒.
如图建立平面直角坐标系,长方形OABC中A(8,0),点C(0,10),点P从原点出发,以每秒1个单位长度的速度沿着O-C-B-A-O的路线运动到点O停止,设点P运动时间为t秒.(1)写出点B的坐标(8,10 ),当t=13时点P坐标为(3,10 )
(2)在点P运动过程中,当点P到x轴的距离为4个单位长度时,则点P运动的时间为4或24秒.
(3)若点P出发11秒时,点Q以每秒2个单位长度的速度也沿着O-C-B-A-O的路线运动到点O停止,求t为何值时点P、Q在运动路线上相距的路程为5个单位长度?并直接写出此时P点的坐标.
分析 (1)根据矩形的性质,可得B点坐标,根据速度乘以时间,可得P点的横坐标,根据平行线的性质,可得P点的纵坐标;
(2)根据速度乘以时间,可得路程,可得OP的长,根据线段的和差,可得AP的长,可得答案;
(3)根据P、Q间的距离,可的关于t的方程,根据解方程,可得答案.
解答 解:(1)由长方形OABC中A(8,0),点C(0,10),得B(8,10),
由OC+CP=13,得CP=3,
P(3,10);
(2)当OP=4时,t=4÷1=4s,
当AP=4时,OC+BC+BP=24,t=24÷1=24s,
故答案为:(8,10),(3,10),4或24;
(3)设P运动了t秒时点P、Q在运动路线上相距的路程为5个单位长度,
当P在前面时,t-2(t-11)=5,解得t=17,P(7,10);
当Q在前面时,2(t-11)-t=5,解得t=27,P(8,1).
点评 本题考查了坐标与图形的性质,利用了矩形的性质,路程、时间、速度的关系,利用两点间的距离得出方程是解题关键,要分类讨论,以防遗漏.

练习册系列答案
相关题目
17.下面的计算错误的是( )
| A. | a3•a3=a6 | B. | (-y2)5=y10 | ||
| C. | (-a3y2)3=-a9y6 | D. | ($\frac{1}{3}$x-$\frac{3}{4}$xy)•(-12y)=-4xy+9xy2 |
15.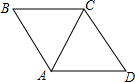 如图,△ABC与△ACD都是等边三角形,△ACD是由△ABC( )
如图,△ABC与△ACD都是等边三角形,△ACD是由△ABC( )
 如图,△ABC与△ACD都是等边三角形,△ACD是由△ABC( )
如图,△ABC与△ACD都是等边三角形,△ACD是由△ABC( )| A. | 绕点A顺时针旋转60°得到的 | B. | 绕点A顺时针旋转120°得到的 | ||
| C. | 绕点C顺时针旋转60°得到的 | D. | 绕点C顺时针旋转120°得到的 |
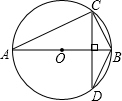 如右图,AB是⊙O的直径,CD是弦,且CD⊥AB,BC=6,AC=8,那么sin∠ABD的值是$\frac{4}{5}$.
如右图,AB是⊙O的直径,CD是弦,且CD⊥AB,BC=6,AC=8,那么sin∠ABD的值是$\frac{4}{5}$.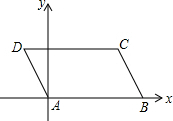 在?ABCD中,AB=5,AD=2,∠DAB=120°,若以点A为原点,直线AB为x轴,如图建立直角坐标系,则C的坐标是(4,$\sqrt{3}$).
在?ABCD中,AB=5,AD=2,∠DAB=120°,若以点A为原点,直线AB为x轴,如图建立直角坐标系,则C的坐标是(4,$\sqrt{3}$).