题目内容
3.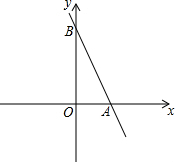 已知直线y=-2x+6与x轴交于点A,与y轴交于点B.
已知直线y=-2x+6与x轴交于点A,与y轴交于点B.(1)点A的坐标为(3,0),点B的坐标为(0,6);
(2)求出△AOB的面积;
(3)直线AB上是否存在一点C(C与B不重合),使△AOC的面积等于△AOB的面积?若存在,求出点C的坐标;若不存在请说明理由.
分析 (1)根据坐标轴上点的坐标特征求A点和B点坐标;
(2)根据三角形面积公式求解;
(3)根据一次函数图象上点的坐标特征,设C(t,-2t+6),则利用三角形面积公式得到$\frac{1}{2}$•3•|-2t+6|=9,然后解绝对值方程求出t的值即可得到C点坐标.
解答 解:(1)当y=0时,-2x+6=0,解得x=3,则A(3,0);
当x=0时,y=-2x+6=6,则B(0,6);
故答案为(3,0),(0,6);
(2)S△OAB=$\frac{1}{2}$×3×6=9;
(3)存在.
设C(t,-2t+6),
∵△AOC的面积等于△AOB的面积,
∴$\frac{1}{2}$•3•|-2t+6|=9,解得t1=6,t2=0(舍去),
∴C点坐标为(6,-6).
点评 本题考查了一次函数图象上点的坐标特征:一次函数y=kx+b,(k≠0,且k,b为常数)的图象是一条直线.它与x轴的交点坐标是(-$\frac{b}{k}$,0);与y轴的交点坐标是(0,b).直线上任意一点的坐标都满足函数关系式y=kx+b.也考查了三角形面积公式.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
15.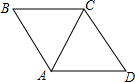 如图,△ABC与△ACD都是等边三角形,△ACD是由△ABC( )
如图,△ABC与△ACD都是等边三角形,△ACD是由△ABC( )
 如图,△ABC与△ACD都是等边三角形,△ACD是由△ABC( )
如图,△ABC与△ACD都是等边三角形,△ACD是由△ABC( )| A. | 绕点A顺时针旋转60°得到的 | B. | 绕点A顺时针旋转120°得到的 | ||
| C. | 绕点C顺时针旋转60°得到的 | D. | 绕点C顺时针旋转120°得到的 |
12.一个工人生产零件,计划30天完成,若每天多生产5个,则在26天里完成且多生产10个.若设原计划每天生产x个,则这个工人原计划每天生产多少个零件?根据题意可列方程( )
| A. | $\frac{30x-10}{x+5}$=26 | B. | $\frac{30x+10}{x+5}$=26 | C. | $\frac{30x}{x+5}$=26+10 | D. | $\frac{30x+10}{x-5}$=26 |
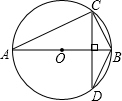 如右图,AB是⊙O的直径,CD是弦,且CD⊥AB,BC=6,AC=8,那么sin∠ABD的值是$\frac{4}{5}$.
如右图,AB是⊙O的直径,CD是弦,且CD⊥AB,BC=6,AC=8,那么sin∠ABD的值是$\frac{4}{5}$.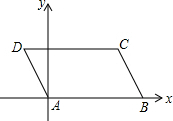 在?ABCD中,AB=5,AD=2,∠DAB=120°,若以点A为原点,直线AB为x轴,如图建立直角坐标系,则C的坐标是(4,$\sqrt{3}$).
在?ABCD中,AB=5,AD=2,∠DAB=120°,若以点A为原点,直线AB为x轴,如图建立直角坐标系,则C的坐标是(4,$\sqrt{3}$).