题目内容
17．
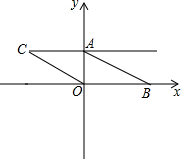如图．已知在平面直角坐标系中．点A（0，m），点B（n，0），D（2m，n），且m、n满足（m-2）2+$\sqrt{n-4}$=0，将线段AB向左平移，使点B与点O重合，点C与点A对应．（1）求点C、D的坐标；
（2）连接CD，动点P从点O出发，以每秒1个单位的速度，沿射线OB方向运动，设点P运动时间为t秒，是否存在某一时刻，使S△PCD=4S△AOB，若存在，请求出t值，并写出P点坐标；若不存在，请说明理由．
分析 （1）根据非负数的性质可求m，n，再根据平移的性质可求点C、D的坐标；
（2）根据三角形面积公式，以及等量关系：S△PCD=4S△AOB，列出关于t的方程求出t值，进一步得到P点坐标即可求解．
解答 解：（1）∵（m-2）2+$\sqrt{n-4}$=0，
∴m-2=0，n-4=0，
解得m=2，n=4，
∴A（0，2），B（4，0），D（4，4），
∵将线段AB向左平移，使点B与点O重合，点C与点A对应，
∴点C的坐标为（-4，2）；
（2）依题意有：
[4-（-4）+t-（-4）]×4÷2-[4-（-4）]×（4-2）÷2-[t-（-4）]×2÷2=4×（4×2÷2），
解得t=4，
则P点坐标为（4，0）．
点评 此题考查了非负数的性质，坐标与图形变化-平移，三角形的面积，解题的关键是得到S△PCD关于t的代数式．
练习册系列答案
相关题目
18．为了迎接郑州市第二届“市长杯”青少年校园足球超级联赛，某学校组织了一次体育知识竞赛．每班选25名同学参加比赛，成绩分别为A、B、C、D四个等级，其中相应等级得分依次记为100分、90分、80分、70分．学校将八年级一班和二班的成绩整理并绘制成统计图，如图所示．
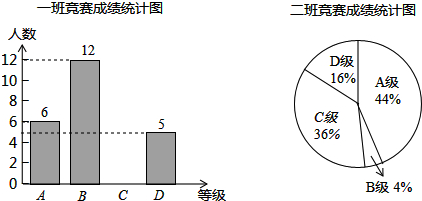
（1）把一班竞赛成绩统计图补充完整；
（2）写出下表中a、b、c的值：
（3）根据（2）的结果，请你对这次竞赛成绩的结果进行分析．
（1）把一班竞赛成绩统计图补充完整；
（2）写出下表中a、b、c的值：
| 平均数（分） | 中位数（分） | 众数（分） | 方差 | |
| 一班 | a | b | 90 | 106.24 |
| 二班 | 87.6 | 80 | c | 138.24 |
如图是一个直角梯形，上底的长是下底长的$\frac{1}{4}$，阴影部分的面积是整个直角梯形面积的80%．
2．
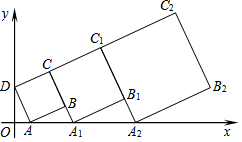在平面直角坐标系中，正方形ABCD的位置如下图所示，点A的坐标为（1，0），点D的坐标为（0，3）．延长CB交x轴于点A1，作正方形A1B1C1C；延长C1B1交x轴于点A2，作正方形A2B2C2C1…按这样的规律进行下去，第2012个正方形的面积为（ ）
在平面直角坐标系中，正方形ABCD的位置如下图所示，点A的坐标为（1，0），点D的坐标为（0，3）．延长CB交x轴于点A1，作正方形A1B1C1C；延长C1B1交x轴于点A2，作正方形A2B2C2C1…按这样的规律进行下去，第2012个正方形的面积为（ ）| A． | $\sqrt{10}$×（$\frac{4}{3}$）4022 | B． | 10×（$\frac{4}{3}$）4022 | C． | 5×（$\frac{4}{3}$）4022 | D． | 10×（$\frac{4}{3}$）4023 |
6．
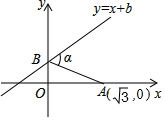如图，已知A点坐标为（$\sqrt{3}$，0），直线y=x+b（b＞0）与y轴交于点B，连接AB，∠α=60°，则b的值为（ ）
如图，已知A点坐标为（$\sqrt{3}$，0），直线y=x+b（b＞0）与y轴交于点B，连接AB，∠α=60°，则b的值为（ ）| A． | 3$\sqrt{3}$-3 | B． | $\sqrt{3}$+3 | C． | 2$\sqrt{3}$+3 | D． | 2$\sqrt{3}$-3 |