题目内容
6. 如图,在△ABC中,已知点D、E、F分别为边BC、AD、CE的中点,且△ABC的面积是4cm2,则阴影部分面积等于( )
如图,在△ABC中,已知点D、E、F分别为边BC、AD、CE的中点,且△ABC的面积是4cm2,则阴影部分面积等于( )| A. | 2cm2 | B. | 1cm2 | C. | $\frac{1}{4}$cm2 | D. | $\frac{1}{2}$cm2 |
分析 因为点F是CE的中点,所以△BEF的底是△BEC的底的一半,△BEF高等于△BEC的高;同理,D、E、分别是BC、AD的中点,△EBC与△ABC同底,△EBC的高是△ABC高的一半;利用三角形的等积变换可解答.
解答  解:如图,点F是CE的中点,
解:如图,点F是CE的中点,
∴△BEF的底是EF,△BEC的底是EC,即EF=$\frac{1}{2}$EC,而高相等,
∴S△BEF=$\frac{1}{2}$S△BEC,
同理得,S△EBC=$\frac{1}{2}$S△ABC,
∴S△BEF=$\frac{1}{4}$S△ABC,且S△ABC=4,
∴S△BEF=1,
即阴影部分的面积为1.
故选B.
点评 本题主要考查了三角形面积的等积变换:若两个三角形的高(或底)相等,其中一个三角形的底(或高)是另一个三角形的几倍,那么这个三角形的面积也是另一个三角形面积的几倍.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
16.下列y关于x的二次函数y=nx2-2x-n(n>0)的图象与x轴的交点的判断中,正确的是( )
| A. | 没有交点 | |
| B. | 只有一个交点,在x轴的负半轴上 | |
| C. | 有两个交点,都在x轴的正半轴 | |
| D. | 有两个交点,分别在x轴的正、负半轴上 |
17.已知直线y=mx+n(m,n为常数)经过点(0,-2)和(3,0),则关于x的方程mx+n=0的解为( )
| A. | x=3 | B. | x=-2 | C. | x=2 | D. | x=0 |
14.下列关于相似的命题中,①等边三角形都相似;②直角三角形都相似;③等腰直角三角形都相似;④矩形都相似,其中真命题有( )
| A. | ①② | B. | ①③ | C. | ①③④ | D. | ①②③④ |
1.要使等式4xy+M=(x+y)2成立,代数式M应为( )
| A. | (x-y)2 | B. | x2-y2 | C. | x2+y2 | D. | (x+y)2 |
11.随着居民经济收入的不断提高以及汽车业的快速发展,家用汽车已越来越多地进入普通家庭,抽样调查发现,截至2016年底某市汽车拥有量为16.9万辆,已知2014年底该市汽车拥有量为10万辆,设2014年底至2016年底该市汽车拥有量的年平均增长率为x,根据题意可列方程得( )
| A. | 10(1-x)2=16.9 | B. | 10(1+2x)=16.9 | C. | 10(1+x)2=16.9 | D. | 16.9(1+x)2=10 |
18.为了迎接郑州市第二届“市长杯”青少年校园足球超级联赛,某学校组织了一次体育知识竞赛.每班选25名同学参加比赛,成绩分别为A、B、C、D四个等级,其中相应等级得分依次记为100分、90分、80分、70分.学校将八年级一班和二班的成绩整理并绘制成统计图,如图所示.
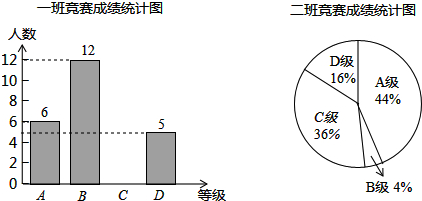
(1)把一班竞赛成绩统计图补充完整;
(2)写出下表中a、b、c的值:
(3)根据(2)的结果,请你对这次竞赛成绩的结果进行分析.

(1)把一班竞赛成绩统计图补充完整;
(2)写出下表中a、b、c的值:
| 平均数(分) | 中位数(分) | 众数(分) | 方差 | |
| 一班 | a | b | 90 | 106.24 |
| 二班 | 87.6 | 80 | c | 138.24 |