题目内容
11.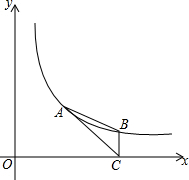 如图,点A,B在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,点A(m,2),点B的横坐标是4,过点B作BC⊥x轴于点C,连接AC,AB.
如图,点A,B在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,点A(m,2),点B的横坐标是4,过点B作BC⊥x轴于点C,连接AC,AB.(1)用含m的式子表示BC,则BC=$\frac{1}{2}$m;
(2)当0<m<4时,求△ABC的面积S(用含m的式子表示);
(3)在(2)的条件下,当△ABC的面积S最大时,求反比例函数y=$\frac{k}{x}$的解析式.
分析 (1)把A坐标代入y=$\frac{k}{x}$求得k=2m,然后把x=4代入求得B的纵坐标,从而求得BC;
(2)根据三角形面积公式即可求得;
(3)把S△ABC=-$\frac{1}{4}$m2+m化成顶点式求得m的值,即可求得解析式.
解答 解:(1)∵点A(m,2)在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,
∴k=2m,
∴y=$\frac{2m}{x}$,
∵点B在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,点B的横坐标是4,过点B作BC⊥x轴于点C,
∴y=$\frac{2m}{4}$=$\frac{1}{2}$m,
∴BC=$\frac{1}{2}$m;
故答案为$\frac{1}{2}$m.
(2)S△ABC=$\frac{1}{2}$•$\frac{1}{2}$m•(4-m)=-$\frac{1}{4}$m2+m(0<m<4);
(3)由S△ABC=-$\frac{1}{4}$m2+m=-$\frac{1}{4}$(m-2)2+1,
∴当m=2时,△ABC的面积S最大,
∴当△ABC的面积S最大时,求反比例函数y=$\frac{k}{x}$的解析式为y=$\frac{4}{x}$.
点评 本题考查了待定系数法求反比例函数的解析式,反比例系数k的几何意义以及反比例函数的性质,熟练掌握待定系数法是解题的关键.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
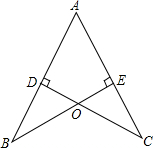 如图,AB=AC,BE⊥AC于点E,CD⊥AB于点D,BE,CD交于点O,试说明:△BDO≌△CEO.
如图,AB=AC,BE⊥AC于点E,CD⊥AB于点D,BE,CD交于点O,试说明:△BDO≌△CEO.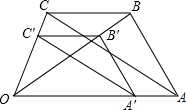 已知:如图,AB∥A′B′,$\frac{B′C′}{BC}$=$\frac{OB′}{OB}$,$\frac{A′C′}{AC}$=$\frac{OA′}{OA}$,试说明:△ABC∽△A′B′C′.
已知:如图,AB∥A′B′,$\frac{B′C′}{BC}$=$\frac{OB′}{OB}$,$\frac{A′C′}{AC}$=$\frac{OA′}{OA}$,试说明:△ABC∽△A′B′C′. 如图,OA⊥OB,∠AOC与∠BOD互补,求∠COD的度数.
如图,OA⊥OB,∠AOC与∠BOD互补,求∠COD的度数.