题目内容
12．设有n个数x1，x2，…xn，其中每个数都可能取0，1，-4三个数中的一个，且x1+x2+…+xn=-2013，x12+x22+…+xn2=2013×19，求x13+x23+…+xn3的值．分析 设该数列中含有a个1，b个-4，根据“x1+x2+…+xn=-2013，x12+x22+…+xn2=2013×19”可列出关于a、b的二元一次方程组，解方程组即可得出a、b的值，再将其代入到x13+x23+…+xn3中即可得出结论．
解答 解：设该数列中含有a个1，b个-4，
根据题意得：$\left\{\begin{array}{l}{a-4b=-2013}\\{a+16b=2013×19}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{a=2013×3}\\{b=2013}\end{array}\right.$．
∴x13+x23+…+xn3=a-64b=-2013×61=-122793．
点评 本题考查了规律型中的数字的变化类以及解二元一次方程组，解题的关键是列出关于a、b的二元一次方程组．本题属于基础题，难度不大，解决该题型题目时，结合数列中数的特点得出方程（或方程组）是关键．
练习册系列答案
相关题目
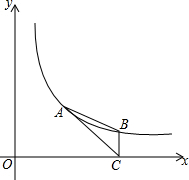如图，点A，B在反比例函数y=$\frac{k}{x}$（k＞0，x＞0）的图象上，点A（m，2），点B的横坐标是4，过点B作BC⊥x轴于点C，连接AC，AB．