题目内容
16.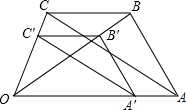 已知:如图,AB∥A′B′,$\frac{B′C′}{BC}$=$\frac{OB′}{OB}$,$\frac{A′C′}{AC}$=$\frac{OA′}{OA}$,试说明:△ABC∽△A′B′C′.
已知:如图,AB∥A′B′,$\frac{B′C′}{BC}$=$\frac{OB′}{OB}$,$\frac{A′C′}{AC}$=$\frac{OA′}{OA}$,试说明:△ABC∽△A′B′C′.
分析 由平行线证出△OAB′∽△OAB,得出对应边成比例$\frac{A′B′}{AB}=\frac{OB′}{OB}=\frac{OA′}{OA}$,再由已知条件得出$\frac{A′B′}{AB}=\frac{B′C′}{BC}=\frac{A′C′}{AC}$,即可得出结论.
解答 证明:∵AB∥A′B′,
∴△OAB′∽△OAB,
∴$\frac{A′B′}{AB}=\frac{OB′}{OB}=\frac{OA′}{OA}$,
∵$\frac{B′C′}{BC}$=$\frac{OB′}{OB}$,$\frac{A′C′}{AC}$=$\frac{OA′}{OA}$,
∴$\frac{A′B′}{AB}=\frac{B′C′}{BC}=\frac{A′C′}{AC}$,
∴△ABC∽△A′B′C′.
点评 本题考查了相似三角形的判定与性质;熟练掌握相似三角形的判定方法,证出两个三角形三边成比例是解决问题的关键.

练习册系列答案
相关题目
6. 如图所示的俯视图是( )
如图所示的俯视图是( )
 如图所示的俯视图是( )
如图所示的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
16.下列各图,不是正方体展开图的是( )
| A. |  | B. |  | C. |  | D. |  |
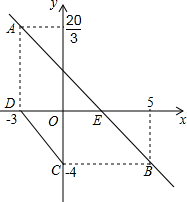 如图,直线y=kx+b经过A(-3,$\frac{20}{3}$)、B(5,-4)两点,过点A作AD⊥x轴于D点,过点B作BC⊥y轴于C点,AB与x轴相交于E点,判断四边形BCDE的形状,并加以证明.
如图,直线y=kx+b经过A(-3,$\frac{20}{3}$)、B(5,-4)两点,过点A作AD⊥x轴于D点,过点B作BC⊥y轴于C点,AB与x轴相交于E点,判断四边形BCDE的形状,并加以证明.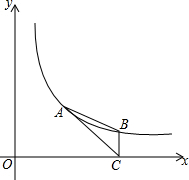 如图,点A,B在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,点A(m,2),点B的横坐标是4,过点B作BC⊥x轴于点C,连接AC,AB.
如图,点A,B在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,点A(m,2),点B的横坐标是4,过点B作BC⊥x轴于点C,连接AC,AB. 如图,在边长为3的正方形ABCD中,E为BC上的一点,且EC=$\frac{1}{3}$BC,过E作EF⊥AE交CD于F,连接AF,把△AEF沿AF翻折到△AGF,使E点落在G处,连接DG,则DG=$\frac{2\sqrt{10}}{5}$.
如图,在边长为3的正方形ABCD中,E为BC上的一点,且EC=$\frac{1}{3}$BC,过E作EF⊥AE交CD于F,连接AF,把△AEF沿AF翻折到△AGF,使E点落在G处,连接DG,则DG=$\frac{2\sqrt{10}}{5}$. 如图,过矩形ABCD的顶点B作BE⊥AC,垂足为E,延长BE交AD于F,若点F是边AD的中点,则sin∠ACD的值是$\frac{\sqrt{6}}{3}$.
如图,过矩形ABCD的顶点B作BE⊥AC,垂足为E,延长BE交AD于F,若点F是边AD的中点,则sin∠ACD的值是$\frac{\sqrt{6}}{3}$.