题目内容
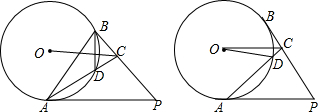
19.如图,PA,PB为⊙O的切线,切点为A、B,OC∥PA交PB于点C,AC交⊙O于点D.(1)连接AB,BD,求证:∠CBD=∠BAC;
(2)连接OD,若$\frac{CD}{AD}$=$\frac{1}{2}$,求tan∠COD的值.
分析 (1)延长BO交⊙O于N,连接DN,欲证明∠CBD=∠BAC,只要证明∠N=∠BAD,∠CBD=∠BAC即可.
(2)连接OA,作DM⊥OC于M,由DM∥OA,设OA=OD=a,得$\frac{DM}{OA}$=$\frac{CD}{CA}$=$\frac{1}{3}$,得DM=$\frac{1}{3}$a,在RT△DOM中利用勾股定理求出OM即可解决问题.
解答 (1)证明:延长BO交⊙O于N,连接DN.
∵PA是⊙O切线,
∴PB⊥NB,
∴∠PBN=90°,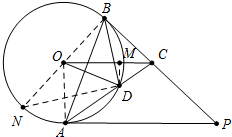
∴∠PBD+∠NBD=90°,
∵BN是直径,
∴∠BDN=90°,
∴∠NBD+∠N=90°,
∴∠PBD=∠N,
∵∠N=∠BAD,
∴∠CBD=∠BAC.
(2)解:连接OA,作DM⊥OC于M.
∵PA是⊙O切线,
∴PA⊥OA,
∵OC∥PA,
∴OC⊥OA,
∵DM⊥OC,AD=2CD,
∴DM∥OA,
设OA=OD=a,
∴$\frac{DM}{OA}$=$\frac{CD}{CA}$=$\frac{1}{3}$,
∴DM=$\frac{1}{3}$a,
在RT△ODM中,∵OD=a,DM=$\frac{1}{3}$a,
∴OM=$\sqrt{O{D}^{2}-D{M}^{2}}$=$\sqrt{{a}^{2}-(\frac{1}{3}a)^{2}}$=$\frac{2\sqrt{2}}{3}$a,
∴tan∠COD=$\frac{DM}{OM}$=$\frac{\frac{1}{3}a}{\frac{2\sqrt{2}}{3}a}$=$\frac{\sqrt{2}}{4}$.
点评 本题考查切线的性质、平行线分线段成比例定理、勾股定理、圆等知识,解题的关键是添加辅助线,构造直角三角形解决问题,题目比较难,属于中考压轴题.

练习册系列答案
相关题目
 如图,将三角板的直角顶点放在直尺的一边上,若∠1=68°,则∠2的度数为22°.
如图,将三角板的直角顶点放在直尺的一边上,若∠1=68°,则∠2的度数为22°.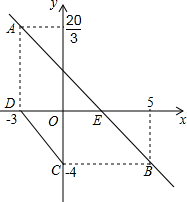 如图,直线y=kx+b经过A(-3,$\frac{20}{3}$)、B(5,-4)两点,过点A作AD⊥x轴于D点,过点B作BC⊥y轴于C点,AB与x轴相交于E点,判断四边形BCDE的形状,并加以证明.
如图,直线y=kx+b经过A(-3,$\frac{20}{3}$)、B(5,-4)两点,过点A作AD⊥x轴于D点,过点B作BC⊥y轴于C点,AB与x轴相交于E点,判断四边形BCDE的形状,并加以证明.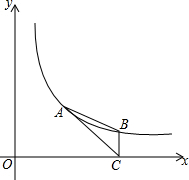 如图,点A,B在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,点A(m,2),点B的横坐标是4,过点B作BC⊥x轴于点C,连接AC,AB.
如图,点A,B在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,点A(m,2),点B的横坐标是4,过点B作BC⊥x轴于点C,连接AC,AB. 如图,过矩形ABCD的顶点B作BE⊥AC,垂足为E,延长BE交AD于F,若点F是边AD的中点,则sin∠ACD的值是$\frac{\sqrt{6}}{3}$.
如图,过矩形ABCD的顶点B作BE⊥AC,垂足为E,延长BE交AD于F,若点F是边AD的中点,则sin∠ACD的值是$\frac{\sqrt{6}}{3}$.