题目内容
2.在Rt△ABC中,∠C=90°,AB:AC=2:1,则∠A的度数是( )| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
分析 首先根据AB:AC=2:1,可得sinB=$\frac{1}{2}$,根据特殊角的三角函数可得∠B=30°,然后再根据直角三角形两锐角互余可得答案.
解答 解:∵Rt△ABC中,∠C=90°,AB:AC=2:1,
∴sinB=$\frac{1}{2}$,
∴∠B=30°.
∴∠A=60°
故选C.
点评 此题主要考查了特殊角的三角函数数值,关键是掌握sin30°=$\frac{1}{2}$.

练习册系列答案
相关题目
12.正六边形的边长等于2,则这个正六边形的面积等于( )
| A. | 4$\sqrt{3}$ | B. | 6$\sqrt{3}$ | C. | 7$\sqrt{3}$ | D. | 8$\sqrt{3}$ |
13.不等式组$\left\{\begin{array}{l}2x+5≤3(x+2)\\ \frac{x-1}{2}<\frac{1}{3}\end{array}\right.$的整数解的个数为( )
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
7.计算[-2(-xn-1)]3=( )
| A. | -2x3n-1 | B. | 8x3n-3 | C. | 16x3n-3 | D. | -16x3n-3 |
11.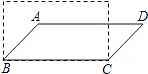 如图,若将四根木条钉成的矩形木框变形为平行四边形ABCD的形状,并使其面积为矩形面积的一半,则这个平行四边形的最小内角等于( )
如图,若将四根木条钉成的矩形木框变形为平行四边形ABCD的形状,并使其面积为矩形面积的一半,则这个平行四边形的最小内角等于( )
 如图,若将四根木条钉成的矩形木框变形为平行四边形ABCD的形状,并使其面积为矩形面积的一半,则这个平行四边形的最小内角等于( )
如图,若将四根木条钉成的矩形木框变形为平行四边形ABCD的形状,并使其面积为矩形面积的一半,则这个平行四边形的最小内角等于( )| A. | 60° | B. | 45° | C. | 30° | D. | 15° |
12.下列说法中不正确的是( )
| A. | 三边长为a、b、c,满足a2-b2=c2的三角形是直角三角形 | |
| B. | 三个角度之比为1:1:$\sqrt{2}$的三角形是直角三角形 | |
| C. | 三个角度之比为1:2:3的三角形是直角三角形 | |
| D. | 三边之比为1:2:$\sqrt{3}$的三角形是直角三角形 |
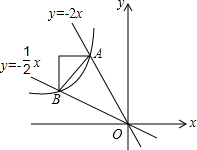 如图,直线y=-2x,y=-$\frac{1}{2}$x交双曲线y=$\frac{k}{x}$于A,B两点(x<0)且S△OAB=4,求k.
如图,直线y=-2x,y=-$\frac{1}{2}$x交双曲线y=$\frac{k}{x}$于A,B两点(x<0)且S△OAB=4,求k.