题目内容
5.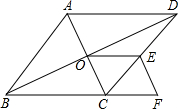 在菱形ABCD中,点O是对角线的交点,E点是边CD的中点,点F在BC延长线上,且CF=$\frac{1}{2}$BC.
在菱形ABCD中,点O是对角线的交点,E点是边CD的中点,点F在BC延长线上,且CF=$\frac{1}{2}$BC.(1)求证:四边形OCEF是平行四边形;
(2)连接DF,如果DF⊥CF,请你写出图中所有的等边三角形.
分析 (1)利用菱形的性质得BO=DO,易得OE是△BDC的中位线,利用中位线的性质得OE∥BC且OE=12BC,利用平行四边形的判定得出结论;
(2)由直角三角形的性质,斜边中线等于斜边的一半得EF=12CD,易得△ECF为等边三角形,利用(1)的结论,易得△OCE为等边三角形,利用等边三角形的性质,得∠ABC=60°,利用判定定理得△ABC与△ADC为等边三角形.
解答 (1)证明:∵四边形ABCD是菱形,
∴BO=DO,
∵E点是边CD的中点,
∴OE是△BDC的中位线,
∴OE∥BC且OE=$\frac{1}{2}$BC,
∵CF=$\frac{1}{2}$BC,
∴OE=CF,
∵OE∥CF,
∴四边形OCFE是平行四边形;
(2)解:∵DF⊥CF,E点是边CD的中点,
∴EF=$\frac{1}{2}CD$,
∵CE=$\frac{1}{2}CD$,
CF=$\frac{1}{2}BC$=$\frac{1}{2}$CD,
∴△ECF为等边三角形;
∵四边形OCFE是平行四边形,
∴OC=EF=CE=CF=OE,
∴△OCE为等边三角形;
∵△ECF为等边三角形,
∴∠ECF=60°,
∴∠ABC=60°,
∵四边形ABCD是菱形,
∴△ABC为等边三角形;
同理得△ADC为等边三角形;
∴图中的等边三角形有:△OCE,△ECF,△ABC,△ADC
点评 本题主要考查了菱形的性质,平行四边形的判定,三角形的中位线定理,等边三角形的判定及性质,综合运用各定理是解答此题的关键.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
15. 将△ABC绕点B逆时针旋转到△A′BC′使A、B、C′在同一直线上,若∠BCA=90°,∠BAC=30°,AB=4cm,则图中阴影部分面积为( )
将△ABC绕点B逆时针旋转到△A′BC′使A、B、C′在同一直线上,若∠BCA=90°,∠BAC=30°,AB=4cm,则图中阴影部分面积为( )
 将△ABC绕点B逆时针旋转到△A′BC′使A、B、C′在同一直线上,若∠BCA=90°,∠BAC=30°,AB=4cm,则图中阴影部分面积为( )
将△ABC绕点B逆时针旋转到△A′BC′使A、B、C′在同一直线上,若∠BCA=90°,∠BAC=30°,AB=4cm,则图中阴影部分面积为( )| A. | $({\frac{16}{3}π-2\sqrt{3}})$cm2 | B. | $({4π-2\sqrt{3}})$cm2 | C. | 4πcm2 | D. | $({4π+2\sqrt{3}})$cm2 |
10.下列数据是2015年4月5日10时公布的中国六大城市的空气污染指数情况:
则这组数据的中位数和众数分别是( )
| 城市 | 天津 | 合肥 | 南京 | 贵阳 | 成都 | 南昌 |
| 污染指数 | 342 | 163 | 165 | 45 | 227 | 163 |
| A. | 185和163 | B. | 164和163 | C. | 185和164 | D. | 163和164 |
 如图,△ABC中,∠ABC=90°,F是AC的中点,过AC上一点D作DE∥AB,交BF的延长线于点E,AG⊥BE,垂足是G,连接BD、AE.
如图,△ABC中,∠ABC=90°,F是AC的中点,过AC上一点D作DE∥AB,交BF的延长线于点E,AG⊥BE,垂足是G,连接BD、AE.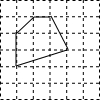 如图,多边形的各顶点都在方格纸的格点(横竖格子线的交错点)上,这样的多边形称为格点多边形,它的面积S可用公式S=a+$\frac{1}{2}$b-1(a是多边形内的格点数,b是多边形边界上的格点数)计算,这个公式称为“皮克定理”.现用一张方格纸共有200个格点,画有一个格点多边形,它的面积S=40.
如图,多边形的各顶点都在方格纸的格点(横竖格子线的交错点)上,这样的多边形称为格点多边形,它的面积S可用公式S=a+$\frac{1}{2}$b-1(a是多边形内的格点数,b是多边形边界上的格点数)计算,这个公式称为“皮克定理”.现用一张方格纸共有200个格点,画有一个格点多边形,它的面积S=40.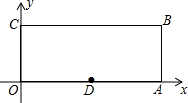 如图,在平面直角坐标系中,O为坐标原点,矩形OABC中,A(10,0),C(0,4),D为OA的中点,P为BC边上一点.若△POD为等腰三角形,则所有满足条件的点P的坐标为(2.5,4),或(3,4),或(2,4),或(8,4).
如图,在平面直角坐标系中,O为坐标原点,矩形OABC中,A(10,0),C(0,4),D为OA的中点,P为BC边上一点.若△POD为等腰三角形,则所有满足条件的点P的坐标为(2.5,4),或(3,4),或(2,4),或(8,4).