题目内容
15.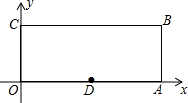 如图,在平面直角坐标系中,O为坐标原点,矩形OABC中,A(10,0),C(0,4),D为OA的中点,P为BC边上一点.若△POD为等腰三角形,则所有满足条件的点P的坐标为(2.5,4),或(3,4),或(2,4),或(8,4).
如图,在平面直角坐标系中,O为坐标原点,矩形OABC中,A(10,0),C(0,4),D为OA的中点,P为BC边上一点.若△POD为等腰三角形,则所有满足条件的点P的坐标为(2.5,4),或(3,4),或(2,4),或(8,4).
分析 由矩形的性质得出∠OCB=90°,OC=4,BC=OA=10,求出OD=AD=5,分情况讨论:①当PO=PD时;②当OP=OD时;③当DP=DO时;根据线段垂直平分线的性质或勾股定理即可求出点P的坐标.
解答 解:∵四边形OABC是矩形,
∴∠OCB=90°,OC=4,BC=OA=10,
∵D为OA的中点,
∴OD=AD=5,
①当PO=PD时,点P在OD得垂直平分线上,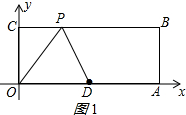
∴点P的坐标为:(2.5,4);
②当OP=OD时,如图1所示:
则OP=OD=5,PC=$\sqrt{{5}^{2}-{4}^{2}}$=3,
∴点P的坐标为:(3,4);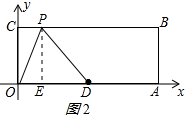 ③当DP=DO时,作PE⊥OA于E,
③当DP=DO时,作PE⊥OA于E,
则∠PED=90°,DE=$\sqrt{{5}^{2}-{4}^{2}}$=3;
分两种情况:当E在D的左侧时,如图2所示:
OE=5-3=2,
∴点P的坐标为:(2,4);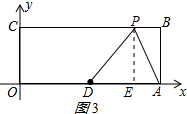 当E在D的右侧时,如图3所示:
当E在D的右侧时,如图3所示:
OE=5+3=8,
∴点P的坐标为:(8,4);
综上所述:点P的坐标为:(2.5,4),或(3,4),或(2,4),或(8,4);
故答案为:(2.5,4),或(3,4),或(2,4),或(8,4).
点评 本题考查了矩形的性质、坐标与图形性质、等腰三角形的判定、勾股定理;本题有一定难度,需要进行分类讨论才能得出结果.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
6.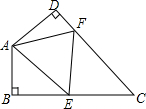 如图,四边形ABCD中,∠C=50°,∠B=∠D=90°,E、F分别是BC、DC上的点,当△AEF的周长最小时,∠EAF的度数为( )
如图,四边形ABCD中,∠C=50°,∠B=∠D=90°,E、F分别是BC、DC上的点,当△AEF的周长最小时,∠EAF的度数为( )
 如图,四边形ABCD中,∠C=50°,∠B=∠D=90°,E、F分别是BC、DC上的点,当△AEF的周长最小时,∠EAF的度数为( )
如图,四边形ABCD中,∠C=50°,∠B=∠D=90°,E、F分别是BC、DC上的点,当△AEF的周长最小时,∠EAF的度数为( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
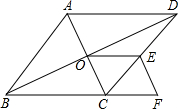 在菱形ABCD中,点O是对角线的交点,E点是边CD的中点,点F在BC延长线上,且CF=$\frac{1}{2}$BC.
在菱形ABCD中,点O是对角线的交点,E点是边CD的中点,点F在BC延长线上,且CF=$\frac{1}{2}$BC.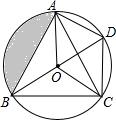 如图,O是△ABC的内心,BO的延长线和△ABC的外接圆相交于点D,连接DC,DA,OA,OC,四边形OADC为平行四边形.
如图,O是△ABC的内心,BO的延长线和△ABC的外接圆相交于点D,连接DC,DA,OA,OC,四边形OADC为平行四边形. 如图,PA是⊙O的切线,A是切点,PA=4,OP=5,则⊙O的周长为6π(结果保留π).
如图,PA是⊙O的切线,A是切点,PA=4,OP=5,则⊙O的周长为6π(结果保留π).
 如图所示,A、B、C三点均在⊙O上,若∠AOB=80°,则∠ACB=40°.
如图所示,A、B、C三点均在⊙O上,若∠AOB=80°,则∠ACB=40°.