题目内容
15．
将△ABC绕点B逆时针旋转到△A′BC′使A、B、C′在同一直线上，若∠BCA=90°，∠BAC=30°，AB=4cm，则图中阴影部分面积为（ ）| A． | $（{\frac{16}{3}π-2\sqrt{3}}）$cm2 | B． | $（{4π-2\sqrt{3}}）$cm2 | C． | 4πcm2 | D． | $（{4π+2\sqrt{3}}）$cm2 |
分析 易得整理后阴影部分面积为圆心角为120°，两个半径分别为4和2的扇形的面积，根据扇形的面积公式即可求解．
解答 解：∵∠BCA=90°，∠BAC=30°，AB=4cm，
∴BC=2，AC=2$\sqrt{3}$，∠A′BA=120°，∠CBC′=120°，
∴阴影部分面积=（S△A′BC′+S扇形BAA′）-S扇形BCC′-S△ABC=$\frac{120π}{360}$×（42-22）=4πcm2．
故选：C．
点评 考查了旋转的性质，扇形面积的计算，本题利用了直角三角形的性质，扇形的面积公式求解．
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
如图，已知⊙O的半径为13，弦AB长为24，则点O到AB的距离是5．
如图，四边形ABCD内接于⊙O，点E在对角线AC上，EC=BC=DC．
3．下列运算中，正确的是（ ）
| A． | 2x-x=2 | B． | x•x4=2x5 | C． | x2y÷y=x2 | D． | （-2x）3=-6x3 |
10．在?ABCD中，AC与BD相交于点O，$\overrightarrow{AB}=\overrightarrow a，\overrightarrow{AD}=\overrightarrow b$，那么$\overrightarrow{AO}$等于（ ）
| A． | $\overrightarrow a+\overrightarrow b$ | B． | $\frac{1}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b$ | C． | $\frac{1}{2}\overrightarrow a-\frac{1}{2}\overrightarrow b$ | D． | $\frac{1}{2}\overrightarrow b-\frac{1}{2}\overrightarrow a$ |
20．-$\sqrt{3}$的倒数是（ ）
| A． | $\sqrt{3}$ | B． | $\frac{1}{\sqrt{3}}$ | C． | -$\frac{1}{\sqrt{3}}$ | D． | -$\frac{1}{3}$ |
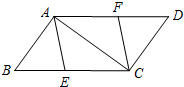如图，已知E、F分别是?ABCD的边BC、AD上的点，且BE=DF．
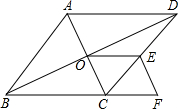在菱形ABCD中，点O是对角线的交点，E点是边CD的中点，点F在BC延长线上，且CF=$\frac{1}{2}$BC．