题目内容
17.如果抛物线y=ax2+bx+c过定点M(1,1),则称此抛物线为定点抛物线.(1)张老师在投影屏幕上出示了一个题目:请你写出一条定点抛物线的一个解析式.小敏写出了一个答案:y=2x2+3x-4,请你写出一个不同于小敏的答案;
(2)张老师又在投影屏幕上出示了一个思考题:已知定点抛物线y=-x2+2bx+c+1,求该抛物线顶点纵坐标的值最小时的解析式,请你解答.
分析 (1)根据顶点式的表示方法,结合题意写一个符合条件的表达式则可;
(2)根据顶点纵坐标得出b=1,再利用最小值得出c=-1,进而得出抛物线的解析式.
解答 解:(1)依题意,选择点(1,1)作为抛物线的顶点,二次项系数是1,
根据顶点式得:y=x2-2x+2;
(2)∵定点抛物线的顶点坐标为(b,c+b2+1),且-1+2b+c+1=1,
∴c=1-2b,
∵顶点纵坐标c+b2+1=2-2b+b2=(b-1)2+1,
∴当b=1时,c+b2+1最小,抛物线顶点纵坐标的值最小,此时c=-1,
∴抛物线的解析式为y=-x2+2x.
点评 本题考查抛物线的形状与抛物线表达式系数的关系,首先利用顶点坐标式写出来,再化为一般形式.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
12.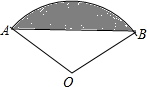 如图所示,扇形AOB的圆心角120°,半径为2,则图中阴影部分的面积为( )
如图所示,扇形AOB的圆心角120°,半径为2,则图中阴影部分的面积为( )
 如图所示,扇形AOB的圆心角120°,半径为2,则图中阴影部分的面积为( )
如图所示,扇形AOB的圆心角120°,半径为2,则图中阴影部分的面积为( )| A. | $\frac{4π}{3}$-2$\sqrt{3}$ | B. | $\frac{4π}{3}$-$\sqrt{3}$ | C. | $\frac{4π}{3}$-$\frac{\sqrt{3}}{2}$ | D. | $\frac{4π}{3}$ |
9.已知x=2是不等式(x-5)(ax-3a+2)≤0的解,且x=1不是这个不等式的解,则实数a的取值范围是( )
| A. | a>1 | B. | a≤2 | C. | 1<a≤2 | D. | 1≤a≤2 |
6.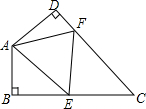 如图,四边形ABCD中,∠C=50°,∠B=∠D=90°,E、F分别是BC、DC上的点,当△AEF的周长最小时,∠EAF的度数为( )
如图,四边形ABCD中,∠C=50°,∠B=∠D=90°,E、F分别是BC、DC上的点,当△AEF的周长最小时,∠EAF的度数为( )
 如图,四边形ABCD中,∠C=50°,∠B=∠D=90°,E、F分别是BC、DC上的点,当△AEF的周长最小时,∠EAF的度数为( )
如图,四边形ABCD中,∠C=50°,∠B=∠D=90°,E、F分别是BC、DC上的点,当△AEF的周长最小时,∠EAF的度数为( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
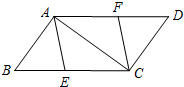 如图,已知E、F分别是?ABCD的边BC、AD上的点,且BE=DF.
如图,已知E、F分别是?ABCD的边BC、AD上的点,且BE=DF.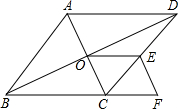 在菱形ABCD中,点O是对角线的交点,E点是边CD的中点,点F在BC延长线上,且CF=$\frac{1}{2}$BC.
在菱形ABCD中,点O是对角线的交点,E点是边CD的中点,点F在BC延长线上,且CF=$\frac{1}{2}$BC.