题目内容
20.在一次翻牌子游戏中,组织者制作了20个牌子,其中有5个牌子的背面注明有奖,其余牌子的背面注明无奖,参与者有三次翻牌的机会,且翻过的牌不能再翻,有一位参与者已翻牌,一次获奖,一次不获奖,那么他第三次翻牌获奖的概率是$\frac{2}{9}$.分析 先计算出前两次翻牌后,现在还有多少个商标牌,其中有奖的有多少个,它们的比值即为所求.
解答 解:∵前两次翻牌后,现在还有18个商标牌,其中有奖的有4个,
∴他第三次翻牌获奖的概率是$\frac{4}{18}=\frac{2}{9}$,
故答案为:$\frac{2}{9}$.
点评 本题考查的是随机事件概率的求法,如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=$\frac{m}{n}$.

练习册系列答案
相关题目
10.在?ABCD中,AC与BD相交于点O,$\overrightarrow{AB}=\overrightarrow a,\overrightarrow{AD}=\overrightarrow b$,那么$\overrightarrow{AO}$等于( )
| A. | $\overrightarrow a+\overrightarrow b$ | B. | $\frac{1}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b$ | C. | $\frac{1}{2}\overrightarrow a-\frac{1}{2}\overrightarrow b$ | D. | $\frac{1}{2}\overrightarrow b-\frac{1}{2}\overrightarrow a$ |
11.甲、乙两班分别由10名选手参加健美比赛,两班参赛选手身高的方差分别是S甲2=1.5,S乙2=2.5,则下列说法正确的是( )
| A. | 甲班选手比乙班选手的身高整齐 | B. | 乙班选手比甲班选手的身高整齐 | ||
| C. | 甲、乙两班选手的身高一样整齐 | D. | 无法确定哪班选手的身高整齐 |
12.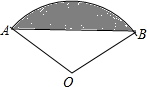 如图所示,扇形AOB的圆心角120°,半径为2,则图中阴影部分的面积为( )
如图所示,扇形AOB的圆心角120°,半径为2,则图中阴影部分的面积为( )
 如图所示,扇形AOB的圆心角120°,半径为2,则图中阴影部分的面积为( )
如图所示,扇形AOB的圆心角120°,半径为2,则图中阴影部分的面积为( )| A. | $\frac{4π}{3}$-2$\sqrt{3}$ | B. | $\frac{4π}{3}$-$\sqrt{3}$ | C. | $\frac{4π}{3}$-$\frac{\sqrt{3}}{2}$ | D. | $\frac{4π}{3}$ |
9.已知x=2是不等式(x-5)(ax-3a+2)≤0的解,且x=1不是这个不等式的解,则实数a的取值范围是( )
| A. | a>1 | B. | a≤2 | C. | 1<a≤2 | D. | 1≤a≤2 |

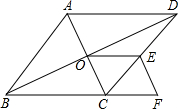 在菱形ABCD中,点O是对角线的交点,E点是边CD的中点,点F在BC延长线上,且CF=$\frac{1}{2}$BC.
在菱形ABCD中,点O是对角线的交点,E点是边CD的中点,点F在BC延长线上,且CF=$\frac{1}{2}$BC.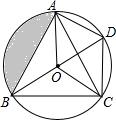 如图,O是△ABC的内心,BO的延长线和△ABC的外接圆相交于点D,连接DC,DA,OA,OC,四边形OADC为平行四边形.
如图,O是△ABC的内心,BO的延长线和△ABC的外接圆相交于点D,连接DC,DA,OA,OC,四边形OADC为平行四边形.