题目内容
在一个直角三角形中,如果有一个锐角为30度,且斜边与较小直角边的和为18cm,求斜边的长.
考点:含30度角的直角三角形
专题:
分析:设斜边为acm,利用含30度的直角三角形的性质可得较小的直角边为
acm,列方程求解即可.
| 1 |
| 2 |
解答:解:设斜边为acm,
∵在直角三角形中,有一个锐角为30度,
∴则较小的直角边为
acm,
∴a+
a=18,解得a=12cm.
∵在直角三角形中,有一个锐角为30度,
∴则较小的直角边为
| 1 |
| 2 |
∴a+
| 1 |
| 2 |
点评:本题主要考查了含30度的直角三角形,解题的关键是熟记含30度的直角三角形中斜边=2×30度的直角所对的边.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
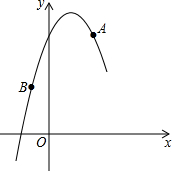 如图,在平面直角坐标系中,抛物线y=ax2+bx+5经过A(2,5),B(-1,2)两点,若点C在该抛物线上,则C点的坐标可能是( )
如图,在平面直角坐标系中,抛物线y=ax2+bx+5经过A(2,5),B(-1,2)两点,若点C在该抛物线上,则C点的坐标可能是( )| A、(-2,0) |
| B、(0.5,6.5) |
| C、(3,2) |
| D、(2,2) |
已知a、b、c为三角形的三边,化简|a+b-c|-|b-a-c|的结果是( )
| A、0 | B、2a |
| C、2(b-c) | D、2(a+c) |
下列方程中,解为x=-3的是( )
| A、5x-14=-1 |
| B、-x+3=0 |
| C、3x+3=2 |
| D、3x+9=0 |
关于x的一元二次方程x2+m=2x,没有实数根,则实数m的取值范围是( )
| A、m<1 | B、m>-1 |
| C、m>1 | D、m<-1 |
 如图,在△ABC中,AB=AC,BD=CD,求证:△ABD≌△ACD.
如图,在△ABC中,AB=AC,BD=CD,求证:△ABD≌△ACD. 如图,在正方形ABCD中,F是DC边的中点,E为BC边上的一点,且EC=
如图,在正方形ABCD中,F是DC边的中点,E为BC边上的一点,且EC=
 如图,△ABC中,点D在BC的延长线上,点F是AB边上一点,延长CA到E,连EF,则∠1,∠2,∠3的大小关系是
如图,△ABC中,点D在BC的延长线上,点F是AB边上一点,延长CA到E,连EF,则∠1,∠2,∠3的大小关系是