题目内容
如图，在正方形ABCD中，F是DC边的中点，E为BC边上的一点，且EC=| 1 |
| 4 |
考点：勾股定理的逆定理,勾股定理
专题：
分析：设FC=a，分别计算AF，EF，AE的值，根据三角形三边长和勾股定理的逆定理可以判定△AEF为直角三角形，即可证明AE⊥EF．
解答：证明：AF⊥EF．
设EC=a，则DC=DA=AB=BC=4a
所以BE=3a，CF=DF=2a．
由勾股定理得AE=5a，
EF=
a，AF=2
a，
∵（
a）2+（2
）2=（5a）2
即EF2+AF2=AE2
∴△AEF为直角三角形，斜边为AE，
故∠AFE=90°，
即AF⊥EF．
设EC=a，则DC=DA=AB=BC=4a
所以BE=3a，CF=DF=2a．
由勾股定理得AE=5a，
EF=
| 5 |
| 5 |
∵（
| 5 |
| 5 |
即EF2+AF2=AE2
∴△AEF为直角三角形，斜边为AE，
故∠AFE=90°，
即AF⊥EF．
点评：本题考查了勾股定理在直角三角形中的运用，考查了正方形各边长相等、各内角为直角的性质，考查了勾股定理的逆定理判定直角三角形的方法，本题中判定△AEF为直角三角形是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
相关题目
将如图所示的“大箭头”按肩头所指的方向平移3厘米，请你作出平移后的图形．
如图，在△ABC中，AB=AC，∠A=120°，BC=8cm，AB的垂直平分线交BC于点M，交AB于点D，AC的垂直平分线交BC于点N，交AC于点E，求MN的长．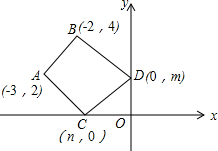
如图，A（-3，2），B（-2，4），C（n，0），D（0，m），若四边形ABCD的周长最小，求-
某学习小组想了解南京市“迎青奥”健身活动的开展情况，准备采用以下调查方式中的一种进行调查：①从一个社区随机选取200名居民；②从一个城镇的不同住宅楼中随机选取200名居民；③从该市公安局户籍管理处随机抽取200名城乡居民作为调查对象．