题目内容
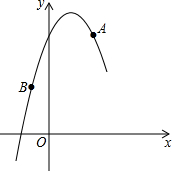如图，在平面直角坐标系中，抛物线y=ax2+bx+5经过A（2，5），B（-1，2）两点，若点C在该抛物线上，则C点的坐标可能是（ ）| A、（-2，0） |
| B、（0.5，6.5） |
| C、（3，2） |
| D、（2，2） |
考点：二次函数图象上点的坐标特征
专题：
分析：因为抛物线过A（2，5），B（-1，2）两点，所以把以上两点的坐标代入求出a和b的值即可求出抛物线的解析式，然后分别把A、B、C、D点的横坐标代入解析式即可判定．
解答：解：把A（2，5），B（-1，2）两点坐标代入得
，
解这个方程组，得
，
故抛物线的解析式为y=-x2+2x+5；
当x=-2时，y=-3，x=0.5时，y=
，x=3时，y=2，x=2时，y=5；
故选C．
|
解这个方程组，得
|
故抛物线的解析式为y=-x2+2x+5；
当x=-2时，y=-3，x=0.5时，y=
| 23 |
| 4 |
故选C．
点评：此题考查了二次函数图象上的坐标特征，待定系数法求函数的解析式，抛物线上点的坐标符合解析式是本题的关键．
练习册系列答案
七星图书口算速算天天练系列答案
初中学业考试导与练系列答案
相关题目
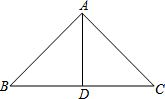下面是小明同学在学了等腰三角形后所做的一道题，题目是这样的：“已知△ABC是等腰三角形，BC边上的高恰好等于BC边长的一半，求∠BAC的度数．”
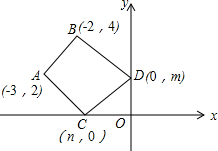如图，A（-3，2），B（-2，4），C（n，0），D（0，m），若四边形ABCD的周长最小，求-
某学习小组想了解南京市“迎青奥”健身活动的开展情况，准备采用以下调查方式中的一种进行调查：①从一个社区随机选取200名居民；②从一个城镇的不同住宅楼中随机选取200名居民；③从该市公安局户籍管理处随机抽取200名城乡居民作为调查对象．
如图，点E是?ABCD的边CB延长线上一点，EA分别交CD、BD的延长线于点F、G，则图中相似三角形共有（ ）对．
下列结论：
①若x=1是关于x的方程a+bx+c=0的一个解，则a+b+c=0；
②若a（x-1）=b（x-1）有唯一的解，则a≠b；
③若b=2a，则关于x的方程ax+b=0（a≠0）的解为x=-
；
④若-a+b+c=1，且a≠0，则x=-1一定是方程ax+b+c=1的解；
其中结论正确个数有（ ）
①若x=1是关于x的方程a+bx+c=0的一个解，则a+b+c=0；
②若a（x-1）=b（x-1）有唯一的解，则a≠b；
③若b=2a，则关于x的方程ax+b=0（a≠0）的解为x=-
| 1 |
| 2 |
④若-a+b+c=1，且a≠0，则x=-1一定是方程ax+b+c=1的解；
其中结论正确个数有（ ）
| A、4个 | B、3个 | C、2个 | D、1个 |
关于x的一元二次方程（m+1）xm2+1+4x+2=0中m的值是（ ）
A、m=-
| ||
| B、m=-1 | ||
| C、m=1 | ||
D、m=
|