Question

5．如图，AB为⊙O的直径，点C是⊙O上一点，BD切⊙O于点B，交AC的延长线于点D，点E为$\widehat{AC}$的中点，连接BE交AC于点F．
（1）求证：△BDF是等腰三角形；
（2）连接AE，若sin∠EAF=$\frac{\sqrt{5}}{5}$，CD=3，求⊙O的半径．

Answer 1

分析 （1）根据点E为$\widehat{AC}$的中点，可以求得∠EBC=∠EAC=∠EBA，由AB为圆的直径，可以求得∠AEB=∠ACB=90°，然后通过转化可以得到所要证明的结论；
（2）根据等角的转化和sin∠EAF=$\frac{\sqrt{5}}{5}$，CD=3，可以分别求得BD、BC的长，从而可以求得AB的长，进而得到圆的半径．

解答 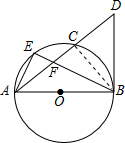（1）证明：连接BC，如右图所示，
∵点E为$\widehat{AC}$的中点，BD切⊙O于点B，
∴∠EBA=∠EAC，∠DBA=90°，
∵AB为⊙O的直径，
∴∠AEB=90°，∠ACB=90°，
∴∠DBF+∠EBA=90°，
又∵∠DFB=∠EFA，∠EFA+∠EAC=90°，
∴∠DFB=∠DBF，
∴△BDF是等腰三角形；
（2）解：设BD=x，
∵CD=3，DF=DB，
∴CF=x-3，
∵∠CBF=∠EAF，sin∠EAF=$\frac{\sqrt{5}}{5}$，∠BCD=90°，
∴设CF=$\sqrt{5}a$，则BF=5a，BC=$2\sqrt{5}a$，
∴$\frac{CF}{BC}=\frac{x-3}{BC}=\frac{\sqrt{5}a}{2\sqrt{5}a}=\frac{1}{2}$，
解得BC=2x-6，
又∵BC=$\sqrt{B{D}^{2}-C{D}^{2}}=\sqrt{{x}^{2}-{3}^{2}}$，
∴2x-6=$\sqrt{{x}^{2}-9}$
解得x=5或x=3（舍去），
即BD=5，BC=4，
∵∠D=∠D，∠DCB=∠DBA=90°，
∴△DCB∽△DBA，
∴$\frac{CD}{BD}=\frac{BC}{AB}$，
即$\frac{3}{5}=\frac{4}{AB}$，
解得AB=$\frac{20}{3}$，
∴⊙O的半径是$\frac{10}{3}$．

点评 本题考查切线的性质，解题的关键是明确题意，找出所求问题需要的条件，利用数形结合的思想解答问题．