题目内容
8. 如图,扇形和正方形ABCD,半径与AB重合,扇形的弧长和AB相等,已知AB=20,扇形沿着正方形翻滚到首次与起始位置相同,则点O经过的路径长为80+80π.
如图,扇形和正方形ABCD,半径与AB重合,扇形的弧长和AB相等,已知AB=20,扇形沿着正方形翻滚到首次与起始位置相同,则点O经过的路径长为80+80π.
分析 不妨设先绕点B逆时针翻滚,点O第一次与正方形的顶点D重合,第二次与正方形顶点C重合,第三次与正方形顶点B重合,第四次与正方形顶点A重合,求出每次翻滚的路径即可解决问题.
解答 解:不妨设先绕点B逆时针翻滚,点O第一次与正方形的顶点D重合,第二次与正方形顶点C重合,第三次与正方形顶点B重合,第四次与正方形顶点A重合,
每次翻滚的路径:当扇形绕B旋转时,路径长是$\frac{180•π•20}{180}$=20π,
当弧NM在BC上时,O经过的路径长是20;
当扇形绕C旋转时,路径长是$\frac{180•π•20}{180}$=20π;
则点O经过的路径长20+20π+20π=20+40π.
所以滚到首次与起始位置相同时,翻滚了四次,路径为80+80π,
点评 本题考查了图形的旋转和弧长的计算公式,理解O经过的路径是本题的关键.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
18. 如图,半径为5的⊙O中,圆心O到弦AB的距离为3,则弦AB的长是( )
如图,半径为5的⊙O中,圆心O到弦AB的距离为3,则弦AB的长是( )
 如图,半径为5的⊙O中,圆心O到弦AB的距离为3,则弦AB的长是( )
如图,半径为5的⊙O中,圆心O到弦AB的距离为3,则弦AB的长是( )| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
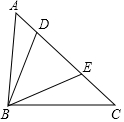 如图,在△ABC中,点D,E是边AC的两点,且满足AE=AB,CB=CD,连接BD,BE,△BDE外接圆的面积为S1,△ABC内切圆的面积为S2,若DE=8,则S1-S2=16π.
如图,在△ABC中,点D,E是边AC的两点,且满足AE=AB,CB=CD,连接BD,BE,△BDE外接圆的面积为S1,△ABC内切圆的面积为S2,若DE=8,则S1-S2=16π. 如图,正方形ABCD的边长为4,点E是边AD上一点,且ED=$\frac{1}{3}$AD,点F在AB上且从点B向点A运动,连接EF并延长交CD的延长线于点G,过点E作EH⊥FG,交BC的延长线于点H,点O是EH的中点,则点O的运动路径长为$\frac{8}{3}$.
如图,正方形ABCD的边长为4,点E是边AD上一点,且ED=$\frac{1}{3}$AD,点F在AB上且从点B向点A运动,连接EF并延长交CD的延长线于点G,过点E作EH⊥FG,交BC的延长线于点H,点O是EH的中点,则点O的运动路径长为$\frac{8}{3}$.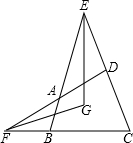 如图,在四边形ABCD中,点E和点F分别是两组对边延长线的交点,EG、FG分别平分∠BEC、∠CFD,且∠ADC=60°,∠ABC=80°,则∠EGF的度数是110°.
如图,在四边形ABCD中,点E和点F分别是两组对边延长线的交点,EG、FG分别平分∠BEC、∠CFD,且∠ADC=60°,∠ABC=80°,则∠EGF的度数是110°.