题目内容
13. 已知:如图,AD是△ABC的高,BE平分∠ABC交AD于E,若∠C=70°,∠BED=68°,求∠BAC的度数.
已知:如图,AD是△ABC的高,BE平分∠ABC交AD于E,若∠C=70°,∠BED=68°,求∠BAC的度数.
分析 由已知条件,首先得出∠DAC=20°,再利用∠ABE=∠EBD,进而得出∠ABE+∠BAE=68°,求出∠EBD,进而得出答案.
解答 解:∵AD是△ABC的高,∠C=70°,
∴∠DAC=20°,
∵BE平分∠ABC交AD于E,
∴∠ABE=∠EBD,
∵∠BED=68°,
∴∠ABE+∠BAE=68°,
∴∠EBD+68°=90°,
∴∠EBD=22°,
∴∠BAE=46°,
∴∠BAC=∠BAE+∠CAD=46°+20°=66°.
点评 此题主要考查了三角形的外角与三角形内角和定理等知识,题目综合性较强,注意从已知条件得出所有结论是解决问题的关键.

练习册系列答案
相关题目
8.为了提倡低碳经济,某公司为了更好得节约能源,决定购买节省能源的10台新机器.现有甲、乙两种型号的设备供选择,其中每台的价格、工作量如下表:
(1)经预算:该公司购买的节能设备的资金不超过110万元,请列式解答有几种购买方案可供选择;
(2)在(1)的条件下,若每月要求产量不低于2040吨,为了节约资金,请你设计一种最省钱的购买方案.
| 甲型 | 乙型 | |
| 价格(万元/台) | 12 | 10 |
| 产量(吨/月) | 240 | 180 |
(2)在(1)的条件下,若每月要求产量不低于2040吨,为了节约资金,请你设计一种最省钱的购买方案.
14.在数轴上,点A所表示的实数为3,点B所表示的实数为a,⊙A的半径为2.那么下列说法中不正确的是( )
| A. | 当a<1时,点B在⊙A外 | B. | 当1<a<5时,点B在⊙A内 | ||
| C. | 当a<5时,点B在⊙A内 | D. | 当a>5时,点B在⊙A外 |

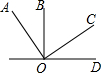 如图,OB⊥OD,OA⊥OC,且∠BOC=58°,则∠AOD的度数为32°.
如图,OB⊥OD,OA⊥OC,且∠BOC=58°,则∠AOD的度数为32°.
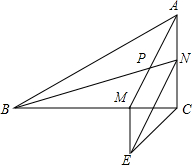 如图,在△ABC中,∠C=90°,AM与BN交于点P,且BM=AC,AN=CM,△EMC是等腰直角三角形,
如图,在△ABC中,∠C=90°,AM与BN交于点P,且BM=AC,AN=CM,△EMC是等腰直角三角形,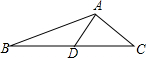 如图△ABC中,点D为BC的中点,AB=5,AC=3,AD=2,则CD长为$\sqrt{13}$.
如图△ABC中,点D为BC的中点,AB=5,AC=3,AD=2,则CD长为$\sqrt{13}$.