题目内容
6.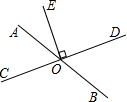 如图,已知直线AB与CD相交于点O,OE⊥CD,则∠AOE与∠DOB互余.
如图,已知直线AB与CD相交于点O,OE⊥CD,则∠AOE与∠DOB互余.
分析 根据垂直的定义,可得∠AOE的度数,根据余角的性质,可得答案.
解答 解:由OE⊥CD,得
∠AOE=90°.
∵∠AOC+∠AOE=90°,∠BOD=∠AOC,
∴∠AOE+∠BOD=90°,
∠AOE与∠DOB 互余,
故答案为:互余.
点评 本题考查了垂线,利用余角的性质是解题关键.

练习册系列答案
相关题目
14.在数轴上,点A所表示的实数为3,点B所表示的实数为a,⊙A的半径为2.那么下列说法中不正确的是( )
| A. | 当a<1时,点B在⊙A外 | B. | 当1<a<5时,点B在⊙A内 | ||
| C. | 当a<5时,点B在⊙A内 | D. | 当a>5时,点B在⊙A外 |
1.函数y=$\sqrt{4-x}$中,自变量x的取值范围( )
| A. | x>4 | B. | x<4 | C. | x≥4 | D. | x≤4 |
16.若一直角三角形的两边长分别为2和4,则第三边长为( )
| A. | 2$\sqrt{3}$ | B. | 2$\sqrt{5}$ | C. | 2$\sqrt{3}$或2$\sqrt{5}$ | D. | 6 |
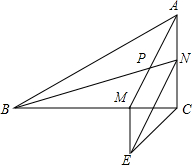 如图,在△ABC中,∠C=90°,AM与BN交于点P,且BM=AC,AN=CM,△EMC是等腰直角三角形,
如图,在△ABC中,∠C=90°,AM与BN交于点P,且BM=AC,AN=CM,△EMC是等腰直角三角形, 如图,在△ABC中,AB=AC=5,BC=8,将△ABC绕着点B旋转的△A′BC′,点A的对应点A′,点C的对应点C′.如果点A′在BC边上,那么点C和点C′之间的距离等于多少$\frac{{8\sqrt{10}}}{5}$.
如图,在△ABC中,AB=AC=5,BC=8,将△ABC绕着点B旋转的△A′BC′,点A的对应点A′,点C的对应点C′.如果点A′在BC边上,那么点C和点C′之间的距离等于多少$\frac{{8\sqrt{10}}}{5}$.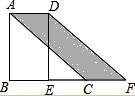 如图,已知在△ABC中,∠B=90°,其面积为12,将△ABC沿BC方向移动至△DEF的位置,若点E为BC的中点,求阴影部分(平行边形CFD)的面积.
如图,已知在△ABC中,∠B=90°,其面积为12,将△ABC沿BC方向移动至△DEF的位置,若点E为BC的中点,求阴影部分(平行边形CFD)的面积.
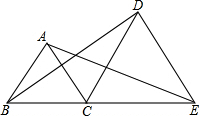 点B、C、E在同一直线上,△ABC和△DCE均为等边三角形,连结AE,DB,求证:AE=DB.
点B、C、E在同一直线上,△ABC和△DCE均为等边三角形,连结AE,DB,求证:AE=DB.