题目内容
16.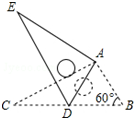 如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上.若BC=2$\sqrt{3}$,∠B=60°,则CD的长为$\sqrt{3}$.
如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上.若BC=2$\sqrt{3}$,∠B=60°,则CD的长为$\sqrt{3}$.
分析 直接利用旋转的性质得出对应边相等,进而利用等边三角形的判定与性质得出AB=AD=BD,AB=$\frac{1}{2}$BC,进而求出答案.
解答 解:∵将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上.
∴AD=AB,
∵∠B=60°,
∴△ADB是等边三角形,∠C=30°,
∴AB=AD=BD,AB=$\frac{1}{2}$BC,
∴AD=BD=$\frac{1}{2}$BC,
∴CD=$\frac{1}{2}$BC=$\sqrt{3}$.
故答案为:$\sqrt{3}$.
点评 此题主要考查了旋转的性质以及等边三角形的判定与性质,得出△ADB是等边三角形是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.若-3xm-3ny8与28y5m+n的和仍是单项式,则有( )
| A. | $\left\{\begin{array}{l}{m=2}\\{n=-2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{m=-2}\\{n=-2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{m=1}\\{n=3}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{m=1}\\{n=-\frac{7}{3}}\end{array}\right.$ |
8.为了提倡低碳经济,某公司为了更好得节约能源,决定购买节省能源的10台新机器.现有甲、乙两种型号的设备供选择,其中每台的价格、工作量如下表:
(1)经预算:该公司购买的节能设备的资金不超过110万元,请列式解答有几种购买方案可供选择;
(2)在(1)的条件下,若每月要求产量不低于2040吨,为了节约资金,请你设计一种最省钱的购买方案.
| 甲型 | 乙型 | |
| 价格(万元/台) | 12 | 10 |
| 产量(吨/月) | 240 | 180 |
(2)在(1)的条件下,若每月要求产量不低于2040吨,为了节约资金,请你设计一种最省钱的购买方案.
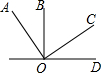 如图,OB⊥OD,OA⊥OC,且∠BOC=58°,则∠AOD的度数为32°.
如图,OB⊥OD,OA⊥OC,且∠BOC=58°,则∠AOD的度数为32°.
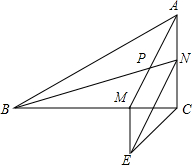 如图,在△ABC中,∠C=90°,AM与BN交于点P,且BM=AC,AN=CM,△EMC是等腰直角三角形,
如图,在△ABC中,∠C=90°,AM与BN交于点P,且BM=AC,AN=CM,△EMC是等腰直角三角形,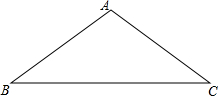 如图,在△ABC中,AB=AC=5,BC=8,将△ABC绕着点B旋转的△A′BC′,点A的对应点A′,点C的对应点C′.如果点A′在BC边上,那么点C和点C′之间的距离等于多少$\frac{{8\sqrt{10}}}{5}$.
如图,在△ABC中,AB=AC=5,BC=8,将△ABC绕着点B旋转的△A′BC′,点A的对应点A′,点C的对应点C′.如果点A′在BC边上,那么点C和点C′之间的距离等于多少$\frac{{8\sqrt{10}}}{5}$.