题目内容
1. 如图所示,正五边形ABCDE的边长为10cm,则对角线AD=5+5$\sqrt{5}$cm.
如图所示,正五边形ABCDE的边长为10cm,则对角线AD=5+5$\sqrt{5}$cm.
分析 连接BE交AD于点F,由正五边形ABCDE,可得∠BAE=108°,∠ABE=∠AEB=∠EAD=36°,求得∠BAF=∠EFD=72°,根据等腰三角形的性质得到ED=DF=10,根据相似三角形的性质即可得到结论.
解答 解:∵五边形ABCDE是正五边形,AB=10,
连接BE交AD于点F,
∵正五边形ABCDE,
可得∠BAE=108°,∠ABE=∠AEB=∠EAD=36°,
∴∠BAF=∠EFD=72°,
∴ED=DF=10,
∵∠AEF=∠EAF,
∴△AEF∽△AED,
∴$\frac{AE}{AD}$=$\frac{AF}{DE}$,
∴$\frac{10}{AD}$=$\frac{AD-10}{10}$,
∴AD=5+5 $\sqrt{5}$cm(负根已经舍弃),
故答案为:5+5 $\sqrt{5}$.
点评 本题考查了正多边形与圆,相似三角形的判定和性质,正确的作出辅助线,寻找相似三角形是解题的关键.

练习册系列答案
相关题目
16.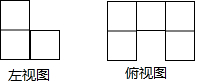 一个由若干相同的小正方形组成的几何体,其左视图和俯视图如图所示,则几何体需要的小正方体个数最多和最少分别是( )
一个由若干相同的小正方形组成的几何体,其左视图和俯视图如图所示,则几何体需要的小正方体个数最多和最少分别是( )
 一个由若干相同的小正方形组成的几何体,其左视图和俯视图如图所示,则几何体需要的小正方体个数最多和最少分别是( )
一个由若干相同的小正方形组成的几何体,其左视图和俯视图如图所示,则几何体需要的小正方体个数最多和最少分别是( )| A. | 最多10个,最少8个 | B. | 最多8个,最少5个 | ||
| C. | 最多8个,最少6个 | D. | 最多15个,最少8个 |
13. 如图,∠ACD为△ABC的一个外角,∠ABC与∠ACD的平分线交于E点,∠A与∠E的关系为( )
如图,∠ACD为△ABC的一个外角,∠ABC与∠ACD的平分线交于E点,∠A与∠E的关系为( )
 如图,∠ACD为△ABC的一个外角,∠ABC与∠ACD的平分线交于E点,∠A与∠E的关系为( )
如图,∠ACD为△ABC的一个外角,∠ABC与∠ACD的平分线交于E点,∠A与∠E的关系为( )| A. | ∠E=90°+$\frac{1}{2}$∠A | B. | ∠E=90°-$\frac{1}{2}$∠A | C. | ∠E=$\frac{1}{2}$∠A | D. | ∠E=2∠A |
8.下列四组数中的三个数能作为直角三角形边长的是( )
| A. | 8,16,17 | B. | 7,12,15 | C. | 12,15,9 | D. | 21,28,25 |

 如图,边长为a正方形OABC的边OA、OC在坐标轴上.在x轴上线段PQ=a(Q在A的右边),P从A出发,以每秒1个单位的速度向O运动,当点P到达点O时停止运动,运动时间为t.连接PB,过P作PB的垂线,过Q作x轴的垂线,两垂线相交于点D.连接BD交y轴于点E,连接PD交y轴于点F,连接PE.
如图,边长为a正方形OABC的边OA、OC在坐标轴上.在x轴上线段PQ=a(Q在A的右边),P从A出发,以每秒1个单位的速度向O运动,当点P到达点O时停止运动,运动时间为t.连接PB,过P作PB的垂线,过Q作x轴的垂线,两垂线相交于点D.连接BD交y轴于点E,连接PD交y轴于点F,连接PE. 重庆八中开展了“书香校园”活动,初三年级某班班长统计了本学期全班50名同学课外图书的阅读数量(单位:本),绘制成折线统计图,在这50名学生的图书阅读数量中,中位数与极差之和是29本.
重庆八中开展了“书香校园”活动,初三年级某班班长统计了本学期全班50名同学课外图书的阅读数量(单位:本),绘制成折线统计图,在这50名学生的图书阅读数量中,中位数与极差之和是29本.