题目内容
13. 如图,∠ACD为△ABC的一个外角,∠ABC与∠ACD的平分线交于E点,∠A与∠E的关系为( )
如图,∠ACD为△ABC的一个外角,∠ABC与∠ACD的平分线交于E点,∠A与∠E的关系为( )| A. | ∠E=90°+$\frac{1}{2}$∠A | B. | ∠E=90°-$\frac{1}{2}$∠A | C. | ∠E=$\frac{1}{2}$∠A | D. | ∠E=2∠A |
分析 根据角平分线的定义、三角形的外角的性质计算即可.
解答 解:∵∠ABC与∠ACD的平分线交于E点,
∴∠EBC=$\frac{1}{2}∠$ABC,∠ECD=$\frac{1}{2}∠$ACD,
∴∠E=∠ECD-∠ECB=$\frac{1}{2}$(∠ACD-∠ABC)=$\frac{1}{2}$∠A,
故选:C.
点评 本题考查的是三角形的外角的性质,掌握三角形的一个外角等于和它不相邻的两个内角的和是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.已知-a+2b+5=0,则2a-4b-3的值是( )
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
8.已知关于x的不等式组$\left\{\begin{array}{l}{x-a≥b}\\{2x-a<2b+1}\end{array}\right.$ 的解集为3≤x<5,则a,b的值为( )
| A. | a=-3,b=6 | B. | a=6,b=-3 | C. | a=1,b=2 | D. | a=0,b=3 |
18.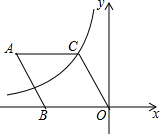 如图,在菱形ABOC中,∠A=60°,它的一个顶点C在反比例函数y=$\frac{k}{x}$的图象上,若将菱形向下平移2个单位,点A恰好落在函数图象上,则反比例函数解析式为( )
如图,在菱形ABOC中,∠A=60°,它的一个顶点C在反比例函数y=$\frac{k}{x}$的图象上,若将菱形向下平移2个单位,点A恰好落在函数图象上,则反比例函数解析式为( )
 如图,在菱形ABOC中,∠A=60°,它的一个顶点C在反比例函数y=$\frac{k}{x}$的图象上,若将菱形向下平移2个单位,点A恰好落在函数图象上,则反比例函数解析式为( )
如图,在菱形ABOC中,∠A=60°,它的一个顶点C在反比例函数y=$\frac{k}{x}$的图象上,若将菱形向下平移2个单位,点A恰好落在函数图象上,则反比例函数解析式为( )| A. | y=-$\frac{{3\sqrt{3}}}{x}$ | B. | y=-$\frac{{\sqrt{3}}}{x}$ | C. | y=-$\frac{3}{x}$ | D. | y=$\frac{{\sqrt{3}}}{x}$ |
3.某股民上周五买进某公司的股票2000股,每股50元,下表为本周每日该股票的涨跌情况(单位:元)
(1)星期二收盘时,每股是多少元?
(2)本周内最高价是每股多少元?最低价是每股多少元?
(3)对该股民本周持股的情况进行分析.
| 星期 | 一 | 二 | 三 | 四 | 五 |
| 每股涨跌 | +5 | +3.5 | -1 | -2.5 | -5.5 |
(2)本周内最高价是每股多少元?最低价是每股多少元?
(3)对该股民本周持股的情况进行分析.
 如图所示,正五边形ABCDE的边长为10cm,则对角线AD=5+5$\sqrt{5}$cm.
如图所示,正五边形ABCDE的边长为10cm,则对角线AD=5+5$\sqrt{5}$cm. 如图,在平面直角坐标系中,边长为1的正方形OA1B1C1的两边在坐标轴上,以它的对角线OB1为边作正方形OB1B2C2,再以正方形OB1B2C2的对角线OB2为边作正方形OB2B3C3,以此类推…,则正方形OBn-1BnCn的顶点Bn的坐标是当k为自然数,如果n=8k+1时,那么Bn(24k,24k);如果n=8k+2时,那么Bn(0,24k+1);如果n=8k+3时,那么Bn(-24k+1,24k+1);如果n=8k+4时,那么Bn(-24k+2,0);如果n=8k+5时,那么Bn(-24k+2,-24k+2);如果n=8k+6时,那么Bn(0,-24k+3);如果n=8k+7时,那么Bn(24k+3,-24k+3);如果n=8k+8时,那么Bn(24k+4,0)..
如图,在平面直角坐标系中,边长为1的正方形OA1B1C1的两边在坐标轴上,以它的对角线OB1为边作正方形OB1B2C2,再以正方形OB1B2C2的对角线OB2为边作正方形OB2B3C3,以此类推…,则正方形OBn-1BnCn的顶点Bn的坐标是当k为自然数,如果n=8k+1时,那么Bn(24k,24k);如果n=8k+2时,那么Bn(0,24k+1);如果n=8k+3时,那么Bn(-24k+1,24k+1);如果n=8k+4时,那么Bn(-24k+2,0);如果n=8k+5时,那么Bn(-24k+2,-24k+2);如果n=8k+6时,那么Bn(0,-24k+3);如果n=8k+7时,那么Bn(24k+3,-24k+3);如果n=8k+8时,那么Bn(24k+4,0)..