题目内容
9．
重庆八中开展了“书香校园”活动，初三年级某班班长统计了本学期全班50名同学课外图书的阅读数量（单位：本），绘制成折线统计图，在这50名学生的图书阅读数量中，中位数与极差之和是29本．
分析 利用折线统计图得到50个数据，其中第25个数为12本，第26个数是18本，从而得到数据的中位数，再求出极差，然后计算它们的和．
解答 解：由折线统计图得这组数据的中位数为15，极差为21-7=14，
所以中位数与极差之和是29本．
故答案为29．
点评 本题考查了折线统计图：折线图是用一个单位表示一定的数量，根据数量的多少描出各点，然后把各点用线段依次连接起来．以折线的上升或下降来表示统计数量增减变化．也考查了中位数和极差．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
明代数学家程大位的《算法统宗》中有这样一个问题（如图），其大意为：有一群人分银子，如果每人分七两，则剩余四两；如果每人分九两，则还差八两，请问：所分的银子共有46两．（注：明代时1斤=16两，故有“半斤八两”这个成语）
20．
如图，一次函数y=kx+b的图象过点（4，1），当y＞1时，x的范围是（ ）
如图，一次函数y=kx+b的图象过点（4，1），当y＞1时，x的范围是（ ）| A． | x＞0 | B． | x＜1 | C． | x＞1 | D． | x＜4 |
17．
一次函数y=kx+b（k，b是常数，k≠0）的图象，如图所示，则不等式kx+b＞0的解集是（ ）
一次函数y=kx+b（k，b是常数，k≠0）的图象，如图所示，则不等式kx+b＞0的解集是（ ）| A． | x＜2 | B． | x＜0 | C． | x＞0 | D． | x＞2 |
4．已知-a+2b+5=0，则2a-4b-3的值是（ ）
| A． | 7 | B． | 8 | C． | 9 | D． | 10 |
14．3-$\sqrt{2}$的倒数是（ ）
| A． | 3+$\sqrt{2}$ | B． | -3+$\sqrt{2}$ | C． | $\frac{3+\sqrt{2}}{4}$ | D． | $\frac{3+\sqrt{2}}{7}$ |
如图所示，正五边形ABCDE的边长为10cm，则对角线AD=5+5$\sqrt{5}$cm．
18．
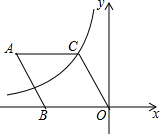如图，在菱形ABOC中，∠A=60°，它的一个顶点C在反比例函数y=$\frac{k}{x}$的图象上，若将菱形向下平移2个单位，点A恰好落在函数图象上，则反比例函数解析式为（ ）
如图，在菱形ABOC中，∠A=60°，它的一个顶点C在反比例函数y=$\frac{k}{x}$的图象上，若将菱形向下平移2个单位，点A恰好落在函数图象上，则反比例函数解析式为（ ）| A． | y=-$\frac{{3\sqrt{3}}}{x}$ | B． | y=-$\frac{{\sqrt{3}}}{x}$ | C． | y=-$\frac{3}{x}$ | D． | y=$\frac{{\sqrt{3}}}{x}$ |
如图，点E、F分别在正方形ABCD的边BC、CD上，∠EAF=45°，则线段BE、EF、FD之间的数量关系为EF=BE+DF．