题目内容
4．已知△ABC∽△DEF，若△ABC与△DEF的相似比为3：2，则△ABC与△DEF的周长比为3：2．分析 根据相似三角形周长的比等于相似比解答．
解答 解：∵△ABC与△DEF的相似比为3：2，
∴△ABC与△DEF的周长比为3：2，
故答案为：3：2．
点评 本题考查的是相似三角形的性质，掌握相似三角形周长的比等于相似比是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
4．把$\frac{{-\sqrt{45{y^2}}}}{{3\sqrt{5y}}}$化简后得（ ）
| A． | $\frac{{-\sqrt{9y}}}{3}$ | B． | $-\sqrt{y}$ | C． | $-3\sqrt{5y}$ | D． | $\frac{{3\sqrt{5}}}{5}$ |
5．
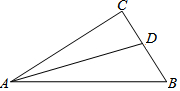如图，在Rt△ABC中，∠C=90°，AD是△ABC的角平分线，若CD=4，AC=12，AB=15，则△ABC的面积为（ ）
如图，在Rt△ABC中，∠C=90°，AD是△ABC的角平分线，若CD=4，AC=12，AB=15，则△ABC的面积为（ ）| A． | 48 | B． | 50 | C． | 54 | D． | 60 |
19．下列性质中，直角三角形具有而等腰三角形不一定具有的是（ ）
| A． | 两边之和大于第三边 | |
| B． | 内角和等于180° | |
| C． | 有两个锐角的和等于90° | |
| D． | 有一个角的平分线垂直于这个角的对边 |
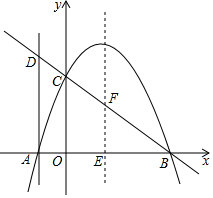如图①已知抛物线y=ax2-3ax+c（a＜0）的图象与x轴交于A、B两点（A在B的左侧），与y的正半轴交于点C，二次函数的对称轴分别与x轴，直线BC交于点E，F，过A作y轴的平行线，与直线BC交于点D，DC：CF=2：3．
如图，已知平行四边形ABCD中，△DEC和△FBC是等边三角形，则∠AEF=60°．