题目内容

5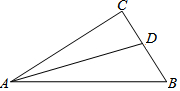．如图，在Rt△ABC中，∠C=90°，AD是△ABC的角平分线，若CD=4，AC=12，AB=15，则△ABC的面积为（　　）
A．48B．50C．54D．60

分析 作DE⊥AB于E，根据角平分线的性质求出DE，根据三角形的面积公式计算即可．

解答 解：作DE⊥AB于E，
∵AD是△ABC的角平分线，∠C=90°，DE⊥AB，
∴DE=CD=4，
∴△ABC的面积为：$\frac{1}{2}$×AC×DC+$\frac{1}{2}$×AB×DE=54，
故选：C．

点评 本题考查的是角平分线的性质，掌握角的平分线上的点到角的两边的距离相等是解题的关键．

练习册系列答案
相关题目
15．如图，线段AB和A1B1线段成中心对称图形（A、B的对称点分别是A1、B1）．在图中用尺规（不写作法，保留作图痕迹）．
（1）作线段AB和A1B1线段的对称中心O；
（2）作△ABC关于点O的中心对称图形．
16．已知：A（0，1），B（1，0），C（3，2）．
（1）求△ABC的面积；
（2）设点P在坐标轴上，且△ABP与△ABC的面积相等，直接写出点P的坐标．
13．计算（-a2）2的结果是（　　）
A．-a6B．-a5C．a4D．a5
20．在体育中考项目中考生可在篮球、排球中选考一项．小明为了选择一项参加体育中考，将自己的10次测验成绩进行比较并制作了折线统计图，依据图中信息小明选择哪一项参加体育中考更合适，并说明理由，篮球，理由：篮球和排球的平均得分相同，但篮球发挥更稳定．
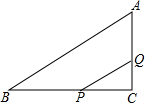10．如图所示，在△ABC中，∠C=90°，BC=8厘米，AC=6厘米，点P从B点出发，以每秒2厘米的速度沿BC向C点移动；点Q从C点出发，以每秒1厘米的速度沿CA向A点移动．
（1）求AB的长；
（2）如果点P、Q分别从B、C同时出发，设运动的时间为x秒，△PCQ的面积为y，求出y关于x的函数解析式，并写出定义域．
（3）当x为何值时，△PCQ是有一个锐角为30°的直角三角形？
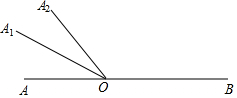7．如图，点O是直线AB上一点，射线OA1，OA2均从OA的位置开始绕点O顺时针旋转，OA1旋转的速度为每秒30°，OA2旋转的速度为每秒10°．当OA2旋转6秒后，OA1也开始旋转，当其中一条射线与OB重合时，另一条也停止．设OA1旋转的时间为t秒．
（1）用含有t的式子表示∠A1OA=（30t）°，∠A2OA=[10（t+6）]°；
（2）当t=1.2，OA1是∠A2OA的角平分线；
（3）若∠A1OA2=30°时，求t的值．
4．已知△ABC∽△DEF，若△ABC与△DEF的相似比为3：2，则△ABC与△DEF的周长比为3：2．
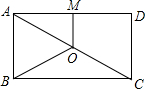5．如图，O是矩形ABCD的对称中心，M是AD的中点．若BC=24，OB=13，则OM的长为5．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网