题目内容
15.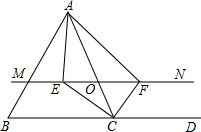 如图所示,△ABC中,点D在BC的延长线上,点O是AC边上的一个动点(不与A,C重合),过点O的直线MN∥BC,CE平分∠ACB交MN于点E,CF平分∠ACD交MN于点F.
如图所示,△ABC中,点D在BC的延长线上,点O是AC边上的一个动点(不与A,C重合),过点O的直线MN∥BC,CE平分∠ACB交MN于点E,CF平分∠ACD交MN于点F.(1)求证:OE=OF.
(2)当点O运动到何处时,四边形AECF是矩形,并说明理由.
分析 (1)根据平行线性质和角平分线性质,由平行线所夹的内错角相等证得即可;
(2)当点O运动到AC的中点时,四边形AECF是矩形,根据矩形的判定方法,即一个角是直角的平行四边形是矩形可证.
解答 证明:(1)∵CE平分∠ACB,
∴∠OCE=∠BCE,
∵MN∥BC,
∴∠ACE=∠BCE,
∴∠OEC=∠BCE,
∴∠OEC=∠OCE,
∴OE=OC,
同理:OF=OC,
∴OE=OF;
(2)当O运动到AC中点时,四边形AECF为矩形;
理由:∵OE=OF,OA=OC
∴四边形AECF为平行四边形
∵∠OCE=$\frac{1}{2}$∠ACB,∠OCF=$\frac{1}{2}$∠ACD
∴∠ECF=∠OCE+∠OCF
=$\frac{1}{2}$∠ACB+$\frac{1}{2}$∠ACD
=$\frac{1}{2}$(∠ACB+∠ACD)
=$\frac{1}{2}$×180°
=90°
∴平行四边形AECF为矩形.
点评 本题涉及矩形的判定定理,解答此类题的关键是要突破思维定势的障碍,运用发散思维,多方思考,探究问题在不同条件下的不同结论,挖掘它的内在联系,向“纵、横、深、广”拓展,从而寻找出添加的条件和所得的结论.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
5.下列运算中错误的是( )
| A. | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{6}$ | B. | $\frac{1}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$ | C. | 2$\sqrt{2}$+3$\sqrt{3}$=5$\sqrt{5}$ | D. | $\sqrt{(-4)^{2}}$=4 |
6.在一次数学阅读课中,小红碰到一个问题:今有鸡兔同笼,上有十七头,下有五十二足,问鸡兔各几何?设x为鸡数,y为兔数,聪明的你请帮她算出x,y的值分别是( )
| A. | $\left\{\begin{array}{l}{x=17}\\{y=52}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=12}\\{y=23}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=8}\\{y=9}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=9}\\{y=8}\end{array}\right.$ |
20.若代数式$\frac{2}{x-2}$和$\frac{3}{2x+1}$的值相等,则x的值为( )
| A. | 3 | B. | 7 | C. | -4 | D. | -8 |
7.下列能用平方差公式计算的是( )
| A. | (-x+y)(x-y) | B. | (y-1)(-1-y) | C. | (x-2)(x+1) | D. | (2x+y)(2y-x) |
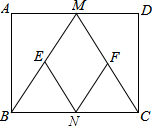 如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是边BM、CM的中点,当AB:AD=1:2时,四边形MENF是正方形.
如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是边BM、CM的中点,当AB:AD=1:2时,四边形MENF是正方形.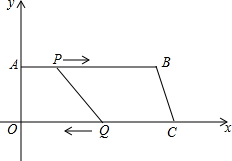 如图,在平面直角坐标系中,四边形OABC的O点为坐标原点,A、C两点分别在y轴和x轴上,AB∥OC,OA=8,AB=24,OC=26,动点P从A开始沿AB边向点D以1个单位/s的速度运动,动点Q从C开始沿CO边向点O以3个单位/s的速度运动,P、Q分别从A、C同时出发,当一点到达时另一点也停止,设运动时间为t.
如图,在平面直角坐标系中,四边形OABC的O点为坐标原点,A、C两点分别在y轴和x轴上,AB∥OC,OA=8,AB=24,OC=26,动点P从A开始沿AB边向点D以1个单位/s的速度运动,动点Q从C开始沿CO边向点O以3个单位/s的速度运动,P、Q分别从A、C同时出发,当一点到达时另一点也停止,设运动时间为t.