题目内容
4.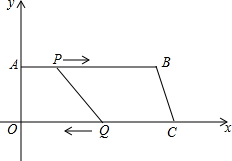 如图,在平面直角坐标系中,四边形OABC的O点为坐标原点,A、C两点分别在y轴和x轴上,AB∥OC,OA=8,AB=24,OC=26,动点P从A开始沿AB边向点D以1个单位/s的速度运动,动点Q从C开始沿CO边向点O以3个单位/s的速度运动,P、Q分别从A、C同时出发,当一点到达时另一点也停止,设运动时间为t.
如图,在平面直角坐标系中,四边形OABC的O点为坐标原点,A、C两点分别在y轴和x轴上,AB∥OC,OA=8,AB=24,OC=26,动点P从A开始沿AB边向点D以1个单位/s的速度运动,动点Q从C开始沿CO边向点O以3个单位/s的速度运动,P、Q分别从A、C同时出发,当一点到达时另一点也停止,设运动时间为t.(1)求直线BC的解析式;
(2)当t为何值时,PQ∥CB?
(3)是否存在t的值,使得PQ将四边形OABC的面积分成2:3两部分?若存在,求出t的值;若不存在,请说明理由.
分析 (1)利用待定系数法即可求解;
(2)PQ∥CB时,四边形PQCB是平行四边形,则PB=QC,据此即可得到关于t的方程,求得t的值;
(3)PQ将四边形OABC的面积分成2:3两部分,即S四边形OABC等于梯形ABCO的$\frac{2}{5}$或$\frac{3}{5}$,根据梯形的面积公式求解.
解答 解:(1)设直线PQ的解析式是y=kx+b,
则$\left\{\begin{array}{l}{24k+b=8}\\{26k+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-4}\\{b=104}\end{array}\right.$,
则直线PQ的解析式是y=-4x+104;
(2)∵PQ∥CD,AB∥OC,
∴四边形PQCB是平行四边形,
∴PB=QC,即24-t=3t,
解得:t=6,
因此,当t=6s时,PQ∥CB;
(3)存在.
∵AP=t,OQ=26-3t,
∴S四边形OAPQ=$\frac{1}{2}$(t+26-3t)×8=-8t+104,
又∵S四边形OABC=$\frac{1}{2}$(24+26)×8=200,
∴-8t+104=$\frac{2}{5}$×200或-8t+104=$\frac{3}{5}$×200,
解得:t=3或-2(舍去).
则当t为3s时,PQ将四边形OABC的面积分成2:3两部分.
点评 本题是待定系数法求一次函数解析式以及梯形的面积的计算的综合题,理解平行四边形的判定定理是关键.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
14.若关于x,y的二元一次方程组$\left\{\begin{array}{l}{x+y=k}\\{2x-y=8k}\end{array}\right.$的解也是二元一次方程3x+2y=10的解,则k的值为( )
| A. | 1 | B. | -2 | C. | 2 | D. | 4 |
12.下列运算中,正确的是( )
| A. | $\sqrt{-2}$×$\sqrt{-3}$=$\sqrt{(-2)×(-3)}$=$\sqrt{6}$ | B. | 2$\sqrt{3}$×3$\sqrt{2}$=6$\sqrt{6}$ | C. | $\sqrt{{a}^{2}-4}$=$\sqrt{{a}^{2}}$-$\sqrt{4}$=a-2 | D. | 3$\sqrt{2}$+2$\sqrt{3}$=5$\sqrt{5}$ |
9.在△ABC中,已知∠A=∠B=45°,BC=$\sqrt{2}$,则边AB的长为( )
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 4 |
16.一个多边形的每个内角均为108°,则这个多边形是( )边形.
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
13.在下列4种正多边形的瓷砖图案中不能铺满地面的是( )
| A. |  | B. |  | C. |  | D. |  |
14.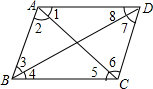 如图,如果AD∥BC,则下列结论正确的是( )
如图,如果AD∥BC,则下列结论正确的是( )
 如图,如果AD∥BC,则下列结论正确的是( )
如图,如果AD∥BC,则下列结论正确的是( )| A. | ∠1=∠4 | B. | ∠2=∠6 | C. | ∠3=∠7 | D. | ∠4=∠8 |
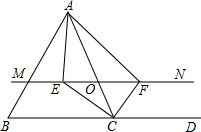 如图所示,△ABC中,点D在BC的延长线上,点O是AC边上的一个动点(不与A,C重合),过点O的直线MN∥BC,CE平分∠ACB交MN于点E,CF平分∠ACD交MN于点F.
如图所示,△ABC中,点D在BC的延长线上,点O是AC边上的一个动点(不与A,C重合),过点O的直线MN∥BC,CE平分∠ACB交MN于点E,CF平分∠ACD交MN于点F.