题目内容
5.你能找出规律吗?(1)计算:$\sqrt{4}×\sqrt{9}$=6,$\sqrt{4×9}$=6.$\sqrt{16}×\sqrt{25}$=20,$\sqrt{16×25}$=20.
(2)请按找到的规律计算:①$\sqrt{5}×\sqrt{20}$; ②$\sqrt{1\frac{2}{3}}×\sqrt{9\frac{3}{5}}$.
(3)已知:a=$\sqrt{2}$,b=$\sqrt{10}$,则$\sqrt{40}$=a2b(用含a,b的式子表示).
分析 (1)首先求出每个算式的值是多少,然后总结出规律:$\sqrt{a}×\sqrt{b}=\sqrt{ab}$(a≥0,b≥0),据此判断即可.
(2)根据$\sqrt{a}×\sqrt{b}=\sqrt{ab}$,可得$\sqrt{5}×\sqrt{20}$=$\sqrt{5×20}=10$,$\sqrt{1\frac{2}{3}}×\sqrt{9\frac{3}{5}}$=$\sqrt{1\frac{2}{3}×9\frac{3}{5}}=\sqrt{16}=4$,据此解答即可.
(3)根据a=$\sqrt{2}$,b=$\sqrt{10}$,可得$\sqrt{40}$=$\sqrt{2×2×10}$=$\sqrt{2}×\sqrt{2}×\sqrt{10}$=a2b,据此解答即可.
解答 解:(1)∵$\sqrt{4}×\sqrt{9}$=6,$\sqrt{4×9}$=6.
$\sqrt{16}×\sqrt{25}$=20,$\sqrt{16×25}$=20.
∴总结出的规律是:
$\sqrt{a}×\sqrt{b}=\sqrt{ab}$(a≥0,b≥0).
(2)∵$\sqrt{a}×\sqrt{b}=\sqrt{ab}$,
∴$\sqrt{5}×\sqrt{20}$=$\sqrt{5×20}=10$,
∴$\sqrt{1\frac{2}{3}}×\sqrt{9\frac{3}{5}}$=$\sqrt{1\frac{2}{3}×9\frac{3}{5}}=\sqrt{16}=4$.
(3)∵a=$\sqrt{2}$,b=$\sqrt{10}$,
∴$\sqrt{40}$=$\sqrt{2×2×10}$=$\sqrt{2}×\sqrt{2}×\sqrt{10}$=a2b.
故答案为:6,6,20,20;a2b.
点评 此题主要考查了算术平方根的性质和应用,要熟练掌握,解答此题的关键是注意观察总结出规律:$\sqrt{a}×\sqrt{b}=\sqrt{ab}$(a≥0,b≥0),并能正确的应用规律.

| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
| A. |  | B. |  | C. |  | D. |  |
| A. | 10组 | B. | 9组 | C. | 8组 | D. | 7组 |
| A. | 3,5,9 | B. | 4,6,8 | C. | 1,$\sqrt{3}$,2 | D. | $\sqrt{3}$,$\sqrt{4}$,$\sqrt{6}$ |
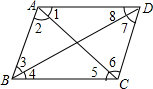 如图,如果AD∥BC,则下列结论正确的是( )
如图,如果AD∥BC,则下列结论正确的是( )| A. | ∠1=∠4 | B. | ∠2=∠6 | C. | ∠3=∠7 | D. | ∠4=∠8 |
| A. | 0.105×109 | B. | 1.05×109 | C. | 1.05×108 | D. | 105×106 |
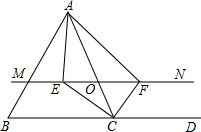 如图所示,△ABC中,点D在BC的延长线上,点O是AC边上的一个动点(不与A,C重合),过点O的直线MN∥BC,CE平分∠ACB交MN于点E,CF平分∠ACD交MN于点F.
如图所示,△ABC中,点D在BC的延长线上,点O是AC边上的一个动点(不与A,C重合),过点O的直线MN∥BC,CE平分∠ACB交MN于点E,CF平分∠ACD交MN于点F.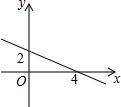 一次函数y=kx+b的图象,如图所示.
一次函数y=kx+b的图象,如图所示.